# 目錄
@[toc]
前言¶
良好的初始化權重有以下的好處:
- 加快梯度下降的收斂速度
- 增加梯度下降收斂到較低訓練(和泛化)錯誤的幾率
所以一個良好的初始化也是非常重要的,這裏嘗試三種初始化化方式:
- 零初始化,將權重參數初始化爲零。
- 隨機初始化,使用隨機的方式,初始化權重參數。
- He初始化,這個公式的初始化方式。
我們來嘗試這個三種方法吧。
模型函數¶
編寫一個model函數,使用這個函數可以測試各種初始化權重參數的效果。
在編寫model函數之前,我們先要導入對於依賴包,其中有些依賴包可以在這裏下載。
# coding=utf-8
import numpy as np
from init_utils import compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset
# 加載圖像數據集:藍色/紅點在圓圈中
train_X, train_Y, test_X, test_Y = load_dataset()
其中使用的數據集是這個樣子的:
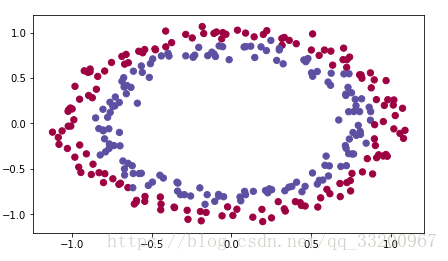
然後就可以編寫model函數了。
def model(X, Y, learning_rate=0.01, num_iterations=15000, print_cost=True, initialization="he"):
"""
實現一個三層神經網絡:LINEAR>RELU->LINEAR->RELU->LINEAR->SIGMOID。
Arguments:
X -- 輸入數據,形狀(2,樣本數量)
Y -- 真正的“標籤”向量(包含0代表紅點;(1)形狀(1,樣本數目)
learning_rate -- 梯度下降的學習速率。
num_iterations -- 運行梯度下降的迭代次數。
print_cost -- 如果是真的,打印每1000次迭代的成本。
initialization -- 選擇使用哪個初始化(“0”、“隨機”或“He”)
Returns:
parameters -- 由模型學習的參數。
"""
global parameters
grads = {}
costs = [] # to keep track of the loss
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 10, 5, 1]
# 字典初始化參數。
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
# 循環(梯度下降)
for i in range(0, num_iterations):
# 前向傳播: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
a3, cache = forward_propagation(X, parameters)
# Loss
cost = compute_loss(a3, Y)
# 反向傳播。
grads = backward_propagation(X, Y, cache)
# 更新參數。
parameters = update_parameters(parameters, grads, learning_rate)
# 每1000次迭代打印一次損失。
if print_cost and i % 1000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
costs.append(cost)
return parameters
零初始化¶
在神經網絡中初始化的參數有兩種類型:
- 權重矩陣 \((W^{[1]}, W^{[2]}, W^{[3]}, ..., W^{[L-1]}, W^{[L]})\)
- 偏差向量 \((b^{[1]}, b^{[2]}, b^{[3]}, ..., b^{[L-1]}, b^{[L]})\)
def initialize_parameters_zeros(layers_dims):
"""
Arguments:
layer_dims——python數組(list),包含每個層的大小。
Returns:
parameters -- 包含參數的python字典 "W1", "b1", ..., "WL", "bL":
W1 -- 形狀權重矩陣(layers_dims[1], layers_dims[0])
b1 -- 形狀偏置向量(layers_dims[1], 1)
...
WL -- 形狀權重矩陣(layers_dims[L], layers_dims[L-1])
bL -- 形狀的偏置向量(layers_dims[L], 1)
"""
parameters = {}
L = len(layers_dims) # 網絡中的層數
for l in range(1, L):
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
然後運行測試一下,會看cost並不怎麼收斂,這是因爲它沒有“破壞對稱性”。
if __name__ == "__main__":
parameters = model(train_X, train_Y, initialization="zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
輸出的日誌信息:
Cost after iteration 0: 0.69314718056
Cost after iteration 1000: 0.69314718056
Cost after iteration 2000: 0.69314718056
Cost after iteration 3000: 0.69314718056
Cost after iteration 4000: 0.69314718056
Cost after iteration 5000: 0.69314718056
Cost after iteration 6000: 0.69314718056
Cost after iteration 7000: 0.69314718056
Cost after iteration 8000: 0.69314718056
Cost after iteration 9000: 0.69314718056
Cost after iteration 10000: 0.69314718056
Cost after iteration 11000: 0.69314718056
Cost after iteration 12000: 0.69314718056
Cost after iteration 13000: 0.69314718056
Cost after iteration 14000: 0.69314718056
On the train set:
Accuracy: 0.5
On the test set:
Accuracy: 0.5
如果使用圖表來顯示的話,是這樣子的:

隨機初始化¶
隨機初始化可以打破對稱,讓我們隨機初始化權重。在隨機初始化之後,每個神經元可以繼續學習其輸入的不同功能。我們只是隨機初始化權重參數,偏差還是繼續初始化爲零。
def initialize_parameters_random(layers_dims):
"""
Arguments:
layer_dims -- python數組(list),包含每個層的大小。
Returns:
parameters -- 包含參數的python字典 "W1", "b1", ..., "WL", "bL":
W1 -- 形狀權重矩陣(layers_dims[1], layers_dims[0])
b1 -- 形狀偏置向量(layers_dims[1], 1)
...
WL -- 形狀權重矩陣(layers_dims[L], layers_dims[L-1])
bL -- 形狀的偏置向量(layers_dims[L], 1)
"""
parameters = {}
L = len(layers_dims) # 表示層數的整數。
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 10
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
運行一下,可以看到已經破壞了對稱性,模型並開始收斂了。
if __name__ == "__main__":
parameters = model(train_X, train_Y, initialization="random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
輸出的日誌如下,看到在0次迭代的時候是“inf”,這是因爲數值舍入的:
Cost after iteration 0: inf
Cost after iteration 1000: 0.386009576858
Cost after iteration 2000: 0.276065073598
Cost after iteration 3000: 0.267517603676
Cost after iteration 4000: 0.261640832949
Cost after iteration 5000: 0.254131922349
Cost after iteration 6000: 0.31200805047
Cost after iteration 7000: 0.243035498545
Cost after iteration 8000: 0.22011133348
Cost after iteration 9000: 0.217258906612
Cost after iteration 10000: 0.214850990347
Cost after iteration 11000: 0.212760572669
Cost after iteration 12000: 0.210936153771
Cost after iteration 13000: 0.209300028106
Cost after iteration 14000: 0.207868192424
On the train set:
Accuracy: 0.883333333333
On the test set:
Accuracy: 0.85
如果用圖表來顯示的話,是這個樣子的:
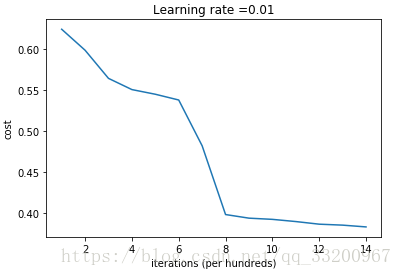
He初始化¶
He初始化跟上面的隨機初始化類似initialize_parameters_random(...)。唯一的區別是,不是np.random.randn(..,..)*10的乘以10,而是乘以\(\sqrt{\frac{2}{\text{dimension of the previous layer}}}\),這是He初始化爲具有ReLU激活的圖層推薦的內容。
def initialize_parameters_he(layers_dims):
"""
Arguments:
layer_dims -- python數組(list),包含每個層的大小。
Returns:
parameters -- 包含參數的python字典 "W1", "b1", ..., "WL", "bL":
W1 -- 形狀權重矩陣(layers_dims[1], layers_dims[0])
b1 -- 形狀偏置向量(layers_dims[1], 1)
...
WL -- 形狀權重矩陣(layers_dims[L], layers_dims[L-1])
bL -- 形狀的偏置向量(layers_dims[L], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims) - 1 # 表示層數的整數
for l in range(1, L + 1):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(
2. / layers_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
運行這個初始化方式。
if __name__ == "__main__":
parameters = model(train_X, train_Y, initialization="he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
輸出的日誌信息是:
Cost after iteration 0: 0.883053746342
Cost after iteration 1000: 0.687982591973
Cost after iteration 2000: 0.675128626452
Cost after iteration 3000: 0.652611776889
Cost after iteration 4000: 0.608295897057
Cost after iteration 5000: 0.530494449172
Cost after iteration 6000: 0.413864581707
Cost after iteration 7000: 0.311780346484
Cost after iteration 8000: 0.236962153303
Cost after iteration 9000: 0.185972872092
Cost after iteration 10000: 0.150155562804
Cost after iteration 11000: 0.123250792923
Cost after iteration 12000: 0.0991774654653
Cost after iteration 13000: 0.0845705595402
Cost after iteration 14000: 0.0735789596268
On the train set:
Accuracy: 0.993333333333
On the test set:
Accuracy: 0.96
如果用圖表來顯示的話,應該是:
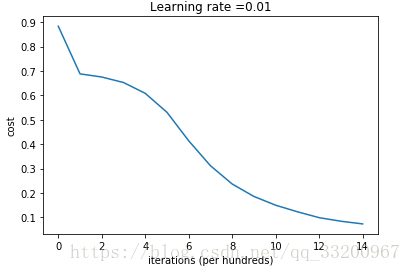
總結¶
最後使用一個表格的方式來總結一下我們使用三個不同的初始化方式的訓練準確率。
| Model | Train accuracy | Problem/Comment | 3-layer NN with zeros initialization | 50% | fails to break symmetry |
| 3-layer NN with large random initialization | 83% | too large weights |
| 3-layer NN with He initialization | 99% | recommended method |
參考資料¶
- http://deeplearning.ai/
該筆記是學習吳恩達老師的課程寫的。初學者入門,如有理解有誤的,歡迎批評指正!