前言

反向传播计算梯度$\frac{\partial J}{\partial \theta}$， $\theta$表示模型的参数。 $J$是使用正向传播和损失函数来计算的。
计算公式如下：

$$
\frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{1}

$$

因为向前传播相对容易实现，所以比较容易获得正确的结果，确定要计算成本$J$ 正确。因此，可以通过计算$J$ 验证计算$\frac{\partial J}{\partial \theta}$ 。

一维梯度检查

一维线性函数$J(\theta) = \theta x$。该模型只包含一个实值参数$\theta$，并采取x作为输入。

上图显示了关键的计算步骤：首先从开始$x$，然后评估该功能 $J(x)$（“前向传播”）。然后计算导数 $\frac{\partial J}{\partial \theta}$（“反向传播”）。下面就用代码来实现。

导入依赖包

首先我们要导入相应的依赖包，其中一些工具类可以在这里下载。

# coding=utf-8
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector

正向传播

下面是线性前向传播函数代码：

def forward_propagation(x, theta):
    """
    实现线性向前传播(计算J) (J(theta) = theta * x)

    Arguments:
    x -- 一个实值输入
    theta -- 我们的参数，一个实数。

    Returns:
    J -- 函数J的值, 计算使用公式 J(theta) = theta * x
    """
    J = theta * x
    return J

反向传播

线性反向传播函数，计算公式是 $dtheta = \frac { \partial J }{ \partial \theta} = x$：

def backward_propagation(x, theta):
    """
    计算J对的导数

    Arguments:
    x -- 一个实值输入
    theta -- 我们的参数，一个实数。

    Returns:
    dtheta -- 成本的梯度。
    """

    dtheta = x

    return dtheta

开始检查

• 在检查梯度之前首先要求$gradapprox$：

1. $\theta^{+} = \theta + \varepsilon$
2. $\theta^{-} = \theta - \varepsilon$
3. $J^{+} = J(\theta^{+})$
4. $J^{-} = J(\theta^{-})$
5. $gradapprox = \frac{J^{+} - J^{-}}{2 \varepsilon}$

• 然后使用反向传播计算梯度，并将结果存储在一个变量“grad”中。
• 最后，使用以下公式计算“gradapprox”和“grad”之间的相对差异：

$$
difference = \frac {\mid\mid grad - gradapprox \mid\mid_2}{\mid\mid grad \mid\mid_2 + \mid\mid gradapprox \mid\mid_2} \tag{2}

$$

如果计算得到的结果足够小，就证明是梯度没问题了，以下是梯度检查代码：

def gradient_check(x, theta, epsilon=1e-7):
    """
    实现反向传播

    Arguments:
    x -- 一个实值输入
    theta -- 我们的参数，一个实数
    epsilon -- 用公式对输入进行微小位移计算近似梯度

    Returns:
    difference -- 近似梯度与反向传播梯度之间的差异。
    """

    # 用公式的左边来计算gradapprox(1)
    thetaplus = theta + epsilon  # Step 1
    thetaminus = theta - epsilon  # Step 2
    J_plus = thetaplus * x  # Step 3
    J_minus = thetaminus * x  # Step 4
    gradapprox = (J_plus - J_minus) / (2 * epsilon)  # Step 5

    # ：检查gradapprox是否足够接近backward_propagation()的输出
    grad = backward_propagation(x, theta)

    numerator = np.linalg.norm(grad - gradapprox)  # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)  # Step 2'
    difference = numerator / denominator  # Step 3'

    if difference < 1e-7:
        print ("梯度是正确的!")
    else:
        print ("梯度是错误的!")

    return difference

然后执行这一段代码，看看梯度是否正确：

if __name__ == "__main__":
    x, theta = 2, 4
    difference = gradient_check(x, theta)
    print("difference = " + str(difference))

当结果满足difference < 1e-7，梯度是正确的。

梯度是正确的!
difference = 2.91933588329e-10

多维梯度检查

多维梯度模型的向前和向后传播如下图：

LINEAR - > RELU - > LINEAR - > RELU - > LINEAR - > SIGMOID

向前传播

多维梯度的向前传播：

def forward_propagation_n(X, Y, parameters):
    """
    实现前面的传播(并计算成本)，如图3所示。

    Arguments:
    X -- m例的训练集。
    Y -- m的样本的标签
    parameters -- 包含参数的python字典 "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- 权重矩阵的形状(5, 4)
                    b1 -- 偏差的矢量形状(5, 1)
                    W2 -- 权重矩阵的形状(3, 5)
                    b2 -- 偏差的矢量形状(3, 1)
                    W3 -- 权重矩阵的形状(1, 3)
                    b3 -- 偏差的矢量形状(1, 1)

    Returns:
    cost -- 成本函数(一个样本的逻辑成本)
    """

    # 检索参数
    m = X.shape[1]
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]

    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)

    # Cost
    logprobs = np.multiply(-np.log(A3), Y) + np.multiply(-np.log(1 - A3), 1 - Y)
    cost = 1. / m * np.sum(logprobs)

    cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)

    return cost, cache

反向传播

多维梯度的反向传播：

def backward_propagation_n(X, Y, cache):
    """
    实现反向传播。

    Arguments:
    X -- 输入数据点，形状(输入大小，1)
    Y -- true "label"
    cache -- 缓存输出forward_propagation_n()

    Returns:
    gradients -- 一个字典，它包含了每个参数、激活和预激活变量的成本梯度。
    """

    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y
    dW3 = 1. / m * np.dot(dZ3, A2.T)
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)

    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1. / m * np.dot(dZ2, A1.T) * 2 # 这有个错误
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)

    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1. / m * np.dot(dZ1, X.T)
    db1 = 4. / m * np.sum(dZ1, axis=1, keepdims=True) # 这有个错误

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
                 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
                 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

开始检查

同样这个还是用回来之前的公式：

$$
\frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{3}

$$

但有一些不同的是，$\theta$ 不再是一个标量。这是一个叫做“参数”的字典。
其中函数是“ vector_to_dictionary”，它输出“参数”字典，操如下图：

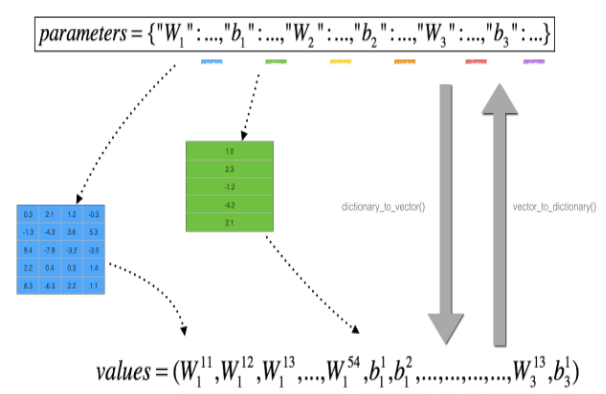
For each i in num_parameters:

• 计算 J_plus[i]:
  1. Set $\theta^{+}$ to np.copy(parameters_values)
  2. Set $\theta^{+}_i$ to $\theta^{+}_i + \varepsilon$
  3. 使用 forward_propagation_n(x, y, vector_to_dictionary($\theta^{+}$ ))计算$J^{+}_i$
• 计算 J_minus[i]：同样计算$\theta^{-}$
• 计算$gradapprox[i] = \frac{J^{+}_i - J^{-}_i}{2 \varepsilon}$

最后使用以下的公式计算结果差异：

$$
difference = \frac {| grad - gradapprox |_2}{| grad |_2 + | gradapprox |_2 } \tag{4}

$$

def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
    """
    检查backward_propagation_n是否正确地计算了正向传播的成本输出的梯度。

    Arguments:
    parameters --包含参数的python字典 "W1", "b1", "W2", "b2", "W3", "b3":
    grad -- backward_propagation_n的输出包含参数的成本梯度。
    x -- 输入数据点，形状(输入大小，1)
    y -- true "label"
    epsilon -- 用公式对输入进行微小位移计算近似梯度

    Returns:
    difference -- 近似梯度与反向传播梯度之间的差异。
    """

    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))

    # Compute gradapprox
    for i in range(num_parameters):
        thetaplus = np.copy(parameters_values)  # Step 1
        thetaplus[i][0] = thetaplus[i][0] + epsilon  # Step 2
        J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus))  # Step 3

        thetaminus = np.copy(parameters_values)  # Step 1
        thetaminus[i][0] = thetaminus[i][0] - epsilon  # Step 2
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus))  # Step 3

        # Compute gradapprox[i]
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)

    # 通过计算与反向传播梯度比较差异。
    numerator = np.linalg.norm(grad - gradapprox)  # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)  # Step 2'
    difference = numerator / denominator  # Step 3'

    if difference > 2e-7:
        print (
            "\033[93m" + "反向传播有一个错误! difference = " + str(difference) + "\033[0m")
    else:
        print (
            "\033[92m" + "你的反向传播效果非常好! difference = " + str(difference) + "\033[0m")

    return difference

最后运行一下这个多维梯度检测：

if __name__ == "__main__":
    X, Y, parameters = gradient_check_n_test_case()
    cost, cache = forward_propagation_n(X, Y, parameters)
    gradients = backward_propagation_n(X, Y, cache)
    difference = gradient_check_n(parameters, gradients, X, Y)

以下是输出结果，可以看到已经超过最低的误差了：

反向传播有一个错误! difference = 0.285093156781

所以我们知道backward_propagation_n的代码有错误！这时我们可以去检查backward_propagation并尝试查找/更正错误，最后我们找到以下的代码出了错误：

dW2 = 1. / m * np.dot(dZ2, A1.T) * 2
db1 = 4. / m * np.sum(dZ1, axis=1, keepdims=True)

然后我们修改正确的代码：

dW2 = 1. / m * np.dot(dZ2, A1.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)

我们再检查一遍的结果是：

你的反向传播效果非常好! difference = 1.18904178766e-07

参考资料

1. http://deeplearning.ai/

该笔记是学习吴恩达老师的课程写的。初学者入门，如有理解有误的，欢迎批评指正！