初步了解TensorFlow

前言
在本章中,我们一起来学习下TensorFlow。我们将会学习到TensorFlow的一些基本库。通过计算一个线性函数来熟悉这些库。最后还学习使用TensorFlow搭建一个神经网络来识别手势。本章用到的一些库在这里下载。
TensorFlow的基本库
首先是导入所需的库,其中最重要的库就是tensorflow的,我们给它一个别名tf。
import math
import numpy as np
import h5py
import tensorflow as tf
from tensorflow.python.framework import ops
from tf_utils import load_dataset, random_mini_batches, convert_to_one_hot, predict
下面我们使用TensorFlow计算一个损失函数,损失函数公式如下:
$$
loss = \mathcal{L}(\hat{y}, y) = (\hat y^{(i)} - y^{(i)})^2 \tag{1}
$$
首先定义两个变量,对应是公式的y帽和y,如下,同时赋值y_hat是36,y是39:
y_hat = tf.constant(36, name='y_hat')
y = tf.constant(39, name='y')
然后根据上面的公式1来定义创建一个计算,其中计算次方非常方便,直接两个星号**:
loss = tf.Variable((y - y_hat)**2, name='loss')
在使用TensorFlow之前,还要先初始化TensorFlow。在执行计算在session中完成。
init = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init)
print(session.run(loss))
经过上面执行,最后输出计算的结果:9
我们通过上面可以看到,TensorFlow定义变量和赋值并不是像我们不同编程一样赋值的了,而是经过TensorFlow的封装,同样计算方式也是一样,如下定义常量和计算也是一样:
a = tf.constant(2)
b = tf.constant(10)
c = tf.multiply(a,b)
print(c)
从上面计算loss可以知道,计算要在session中执行。所以我们这里不会输出结果20,而是输出c的张量:Tensor("Mul:0", shape=(), dtype=int32)
要计算它们的值,还有在session中run才行,如下:
sess = tf.Session()
print(sess.run(c))
最后会输出正确的结果:20。
上面都是一开始就指定变量的值的,但是有些情况下,我们是一开始是不用指定值的,那么我们怎么处理了,这样就用到了占位符,如下:
x = tf.placeholder(tf.int64, name = 'x')
print(sess.run(2 * x, feed_dict = {x: 3}))
sess.close()
这里一开始我们没有指定x的值,而是在run的时候,使用一个feed_dict字典的方式给x赋值。
常用计算
线性函数
下面来介绍计算线性函数的方法,下面是线性函数的公式:
$$
Y = WX + b\tag{2}
$$
使用的的函数如下:
tf.matmul()做一个矩阵乘法tf.add()做一个加法np.random.randn()随机初始化
def linear_function():
# 随机生成一个对应的张量
X = tf.constant(np.random.randn(3,1), name = "X")
W = tf.constant(np.random.randn(4,3), name = "W")
b = tf.constant(np.random.randn(4,1), name = "b")
# 生成线性函数
Y = tf.add(tf.matmul(W, X), b)
# 开始计算线性函数
sess = tf.Session()
result = sess.run(Y)
# 如果没使用with的话,还要关闭session
sess.close()
return result
计算sigmoid函数
这是一个计算sigmoid函数,使用TensorFlow自带函数,无需自己定义:
def sigmoid(z):
# 给x创建一个占位符,并指定类型
x = tf.placeholder(tf.float32, name = "x")
# 使用TensorFlow自带的sigmoid函数
sigmoid = tf.sigmoid(x)
with tf.Session() as sess:
# 使用传进来的值计算
result = sess.run(sigmoid, feed_dict = {x: z})
return result
计算损失函数
损失函数的计算公式如下:
$$
J = - \frac{1}{m} \sum_{i = 1}^m \large ( \small y^{(i)} \log a^{ [2] (i)} + (1-y^{(i)})\log (1-a^{ [2] (i)} )\large )\small\tag{3}
$$
可以通过直接调用tf.nn.sigmoid_cross_entropy_with_logits()函数定义完成损失函数的计算:
def cost(logits, labels):
# 定义两个占位符
z = tf.placeholder(tf.float32, name = "z")
y = tf.placeholder(tf.float32, name = "y")
# 使用TensorFlow自带函数计算交叉熵损失
cost = tf.nn.sigmoid_cross_entropy_with_logits(logits = z, labels = y)
# 创建session
sess = tf.Session()
# 开始计算损失值
cost = sess.run(cost, feed_dict = {z: logits, y: labels})
# 关闭session
sess.close
return cost
独热编码
独热编码即 One-Hot 编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。如下图所示:
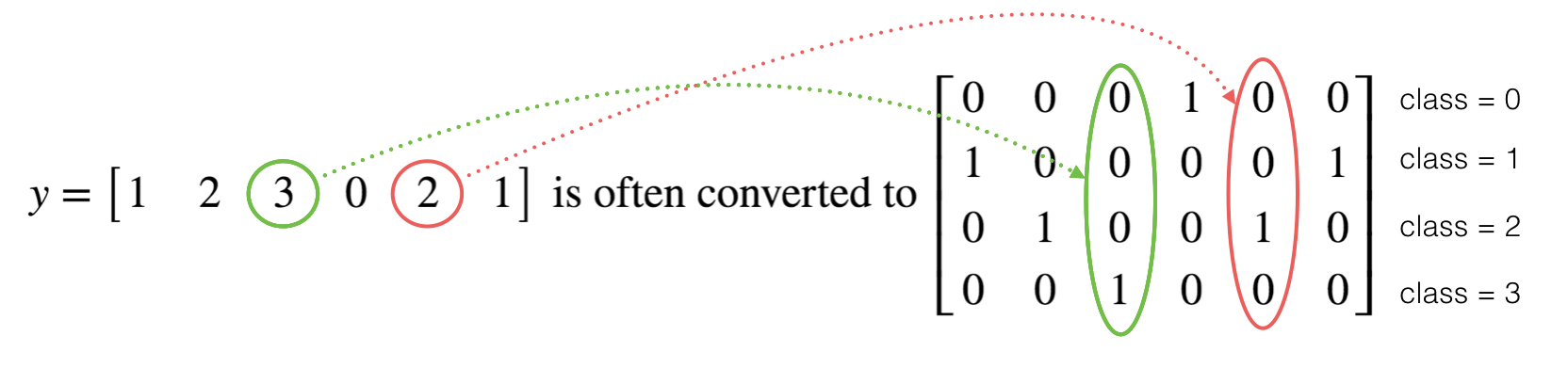
在TensorFlow中可以使用tf.one_hot(标签,深度,轴)创建独热编码,使用TensorFlow如下:
def one_hot_matrix(labels, C):
# 定义深度常量
C = tf.constant(C, name = "C")
# 创建独热编码矩阵
one_hot_matrix = tf.one_hot(labels, C, axis = 0)
# 创建Session
sess = tf.Session()
# 计算独热编码
one_hot = sess.run(one_hot_matrix)
# 关闭session
sess.close
return one_hot
我们测试一下,看看效果:
labels = np.array([1,2,3,0,2,1])
# 4个深度,也就是4个类别
one_hot = one_hot_matrix(labels, C = 4)
print ("one_hot = " + str(one_hot))
输出结果如下:
one_hot = [[ 0. 0. 0. 1. 0. 0.]
[ 1. 0. 0. 0. 0. 1.]
[ 0. 1. 0. 0. 1. 0.]
[ 0. 0. 1. 0. 0. 0.]]
初始化矩阵
可以使用TensorFlow自带函数创建1矩阵:
def ones(shape):
# 根据形状大小传1矩阵
ones = tf.ones(shape)
# 获取Session
sess = tf.Session()
# 在session中运行
ones = sess.run(ones)
# 关闭session
sess.close
return ones
TensorFlow创建神经网络
使用TensorFlow创建一个神经网络,来识别手势。我们可以使用独热编码当做图像的标签。

首先是加载数据:
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
对数据进行扁平化和归一化:
# 训练和测试图像
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T
# 归一化图像向量
X_train = X_train_flatten/255.
X_test = X_test_flatten/255.
# 将训练和测试标签转换为独热矩阵
Y_train = convert_to_one_hot(Y_train_orig, 6)
Y_test = convert_to_one_hot(Y_test_orig, 6)
为输入数据和输出结果定义一个占位符:
def create_placeholders(n_x, n_y):
# 输入数据占位符
X = tf.placeholder(dtype=tf.float32,shape=(n_x, None), name = "Placeholder_1")
# 输出数据占位符
Y = tf.placeholder(dtype=tf.float32,shape=(n_y, None), name = "Placeholder_2")
return X, Y
初始化参数:
def initialize_parameters():
# 初始化权重和偏置值
W1 = tf.get_variable("W1", [25,12288], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b1 = tf.get_variable("b1", [25,1], initializer = tf.zeros_initializer())
W2 = tf.get_variable("W2", [12,25], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b2 = tf.get_variable("b2", [12,1], initializer = tf.zeros_initializer())
W3 = tf.get_variable("W3", [6,12], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b3 = tf.get_variable("b3", [6,1], initializer = tf.zeros_initializer())
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
"W3": W3,
"b3": b3}
return parameters
计算正向传播:
def forward_propagation(X, parameters):
# 获取权重和偏差值
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
# 相当于 Z1 = np.dot(W1, X) + b1
Z1 = tf.add(tf.matmul(W1, X), b1)
# 计算RELU A1 = relu(Z1)
A1 = tf.nn.relu(Z1)
# 相当于 Z2 = np.dot(W2, a1) + b2
Z2 = tf.add(tf.matmul(W2, A1), b2)
# 计算RELU A2 = relu(Z2)
A2 = tf.nn.relu(Z2)
# 相当于 Z3 = np.dot(W3,Z2) + b3
Z3 = tf.add(tf.matmul(W3, A2), b3)
return Z3
计算损失:
def compute_cost(Z3, Y):
# 转置,为下面计算计算损失做准备
logits = tf.transpose(Z3)
labels = tf.transpose(Y)
# 传入的值是数据和标签
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = labels))
return cost
计算反向传播和更新参数,使用框架的话,只要使用下面两行代码就可以了:
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)
_ , c = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
创建模型
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,
num_epochs = 1500, minibatch_size = 32, print_cost = True):
"""
3层神经网络: LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX.
Arguments:
X_train -- 训练数据集,输入大小为12288,输入数量为1080
Y_train -- 训练标签,输入大小为6,输入数量为1080
X_test -- 训练数据集,输入大小为12288,输入数量为120
Y_test -- 训练标签,输入大小为6,输入数量为120
learning_rate -- 学习速率的优化
num_epochs -- 优化循环的周期数
minibatch_size -- minibatch大小
print_cost -- 每100个pass就打印成本
Returns:
parameters -- 由模型学习的参数。他们可以被用来预测。
"""
ops.reset_default_graph()
tf.set_random_seed(1)
seed = 3
# n_x:输入大小,m:数据集样本
(n_x, m) = X_train.shape
# 输出大小
n_y = Y_train.shape[0]
costs = []
# 创建输入输出占位符
X, Y = create_placeholders(n_x, n_y)
# 初始化参数
parameters = initialize_parameters()
# 计算正向传播
Z3 = forward_propagation(X, parameters)
# 计算损失值
cost = compute_cost(Z3, Y)
# 反向传播,定义优化方法吗,使员工Adam作为优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)
# 初始化所有的变量
init = tf.global_variables_initializer()
# 在Session中计算
with tf.Session() as sess:
# 运行初始化
sess.run(init)
# 在循环中训练
for epoch in range(num_epochs):
epoch_cost = 0.
# 计算小批量的数量
num_minibatches = int(m / minibatch_size)
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
# 把每个批量的数据拆分
(minibatch_X, minibatch_Y) = minibatch
# 在session中运行优化器和Cost
_ , minibatch_cost = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
epoch_cost += minibatch_cost / num_minibatches
# 打印cost
if print_cost == True and epoch % 100 == 0:
print ("Cost after epoch %i: %f" % (epoch, epoch_cost))
if print_cost == True and epoch % 5 == 0:
costs.append(epoch_cost)
# 参数保存在一个变量中
parameters = sess.run(parameters)
print ("Parameters have been trained!")
# 计算正确的预测
correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))
# 计算测试集的准确性。
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))
return parameters
最后通过调用该函数即可完成训练:
parameters = model(X_train, Y_train, X_test, Y_test)
预测,训练好的参数就可以用来预测了,如下:
import scipy
from PIL import Image
from scipy import ndimage
my_image = "thumbs_up.jpg"
# 预先处理图像以适应的算法
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64)).reshape((1, 64*64*3)).T
my_image_prediction = predict(my_image, parameters)
print("Your algorithm predicts: y = " + str(np.squeeze(my_image_prediction)))
参考资料
该笔记是学习吴恩达老师的课程写的。初学者入门,如有理解有误的,欢迎批评指正!