目錄¶

@[toc]

深度學介紹¶

AI比喻新電是是因爲AI就像大約100年前的電力一樣，正在改變多個行業，如：汽車行業，農業和供應鏈。
深度學習最近起飛的原因是：硬件的開發，特別是GPU的計算，是我們獲得更多的計算能力；深度學習已在一些重要的領域應用，如廣告，語音識別和圖像識別等等；目前數字化的時代使得我們擁有更多的數據。
關於迭代不同ML思想的圖：

- 這個思維圖能夠快速嘗試想法，可以讓深度學習工程師更快速地迭代自己的想法；
- 可以加快團隊迭代一個主意的時間；深度學習算法的新進展使得我們能更好地訓練模型，即使不改變CPU或者GPU硬件。
尋找模型的特徵是獲取良好性能的關鍵，雖然經驗可以提供幫助，但是需要多次迭代來建立一個良好的模型。
ReLU激活函數的圖表如下：
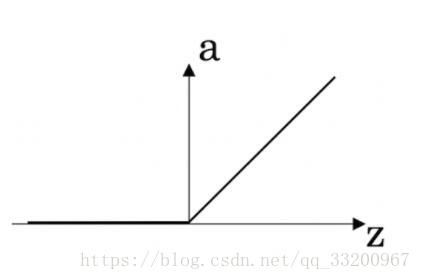
貓的識別是一個“非結構化”的數據例子；統計不同城市人口，人均GDP，經濟增長的人口統計數據集是反映圖像，音頻或者文本數據集的“結構化”數據的一個例子。
爲什麼使用RNN（循環神經網絡）作爲機器翻譯，這是因爲RNN是一個可以被訓練的監督學習的問題；RNN的輸入和輸出是一個序列，翻譯就是從一種語言序列映射到另一種語言的序列。
這張手工繪製的圖像，x軸是指數據量，y軸是指算法的性能
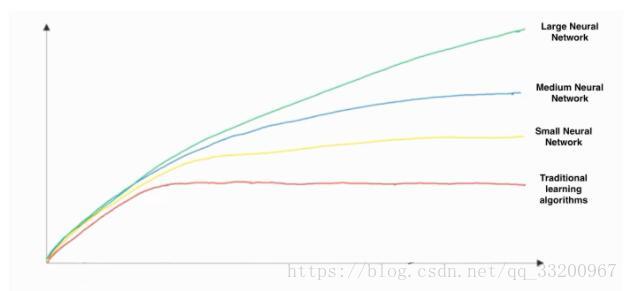
- 同時在圖像中可以看出增加訓練數據是不會影響算法的性能的，引入更多的數據對模型總是有益的；
- 有知道增加神經網絡的大小通常不會影響算法的性能，大型的網絡通常比小網絡表現要好。

神經網絡基礎¶

神經元計算一個線性函數(z = Wx + b),後跟一個激活函數（sigmoid，tanh，ReLU，…）
使用numpy直接計算矩陣，這跟np.dot(a,b)不同，直接運算時按照廣播的方式運算的，使員工np.dot(a,b)是按照平時矩陣的計算方式的。
假設img是一個(32,32,3)的數組，代表具有3個顏色通道紅色，綠色和藍色的3232的圖像，重塑這個成爲列向量應該爲：x = img.reshape((3232*3,1))
“Logistic Loss”函數應該是：
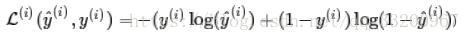
以下圖像的計算過程

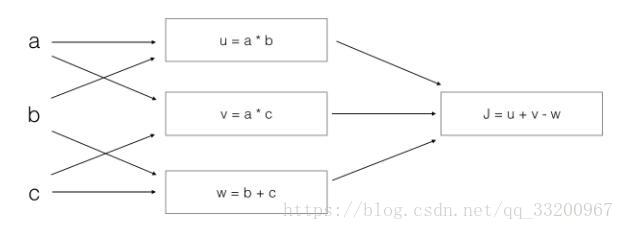
應該是：
$$
J = u + v - w = (ab)+(ac)-(b+c)
= a(b+c)-(b+c) = (a-1)(b+c)
$$

淺層神經網絡¶

$a^{[12](2)}$表示激活向量的第2層的第12個的訓練樣本。
$X$每列都是一個訓練樣本的矩陣
$a_4^{[2]}$表示第2層的第4個的激活輸出
$a^{[2]}$表示第2層激活向量
tanh激活函數通常比隱層單元的sigmoid激活函數效果要好，因爲tanh的輸出範圍在(-1,1)，其平均值更接近零，因此它能把數據更集中傳到下一層，使學習變得更簡單。
Sigmoid函數的輸出在0和1之間，這使得它是二分類的非常好的一個選擇，當輸出低於0.5時，可以歸類爲0；當輸出高於0.5時，可以歸類爲1。使用tanh函數也可以，但是tanh的函數在-1和1之間，操作不太方便。
Logistic迴歸因爲沒有隱層，如果將權重初始化爲零，則Logistic迴歸中的第一個樣本輸出將是零，但是Logistic迴歸的導數取決於不是零，而是輸入的x(因爲沒有隱層)。因此在第二次迭代中，如果x不是常量向量，則權重值遵循x的分佈且彼此不同。
當tanh激活函數的輸入遠離零時，其梯度就非常接近於零，因爲此時的tanh斜率接近零。
一個隱藏層的神經網絡：

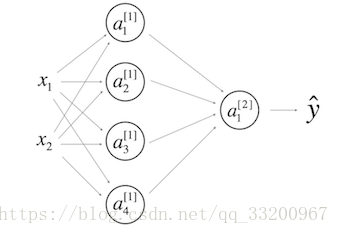
$b^{[1]}$的形狀應該是(4,1)；$b^{[2]}$的形狀應該是(1,1)；$W^{[1]}$的形狀應該是(4,2)；$W^{[2]}$形狀應該是(1,4)
在$l$層中，其中$1<=l<=L$，對$l$層前向傳播正確矢量化的公式是：

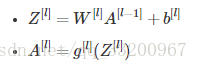
深度神經網絡¶

在前向傳播和反向傳播中使用“cache”，是爲了記錄前向傳播單元計算的值，然後傳送給反向傳播的單元，因爲在使用鏈式法則計算導數時使用到。
屬於超參數的是：迭代次數，學習率，神經網絡$L$的層數，隱層的數量。
深層神經網絡比淺層神經網絡計算更加複雜的輸入特徵。
以下這個網絡是4層的神經網絡，有3個隱層

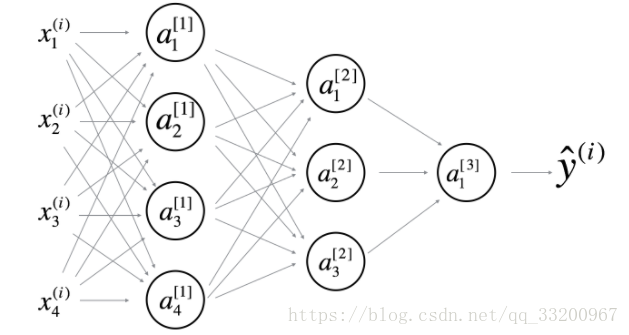
計算層數的方式：層數=隱層+1，輸入層和輸出層不屬於隱層。
在前向傳播中，前向函數需要知道使用的是什麼激活函數（Sigmoid，tanh，ReLU，等等），因爲在反向傳播中需要知道是使用了什麼激活函數才能正確計算導數。
使用淺層網絡電路進行計算，需要一個大型的網絡（我們通過網絡的邏輯門數來測量大小），但是計算深層的電路的話，只需要一個指數規模比較小的網絡。
以下是一個2層隱層的神經網絡結構圖：
[外鏈圖片轉存失敗(img-ggjHJvwx-1563949655959)(https://note.youdao.com/yws/api/personal/file/AE2D93A09BC54E4AB3A986056C2B4DDB?method=download&shareKey=2e6f6ed04ebd0c5c7e5e3fa21d71b3f2)]
它具有：(i)、$W^{[1]}$的形狀是(4,4)（計算方式是：$W^{[l]} = (n^{[l]},n^{[l-1]})$），同樣$W^{[2]}$的形狀是(3,4)，$W^{[3]}$的形狀是(1,3)；(ii)、$b^{[1]}$的形狀是(4,1)（計算方式是：$b^{[l]} = (n^{[l]},1)$），同樣$b^{[2]}$的形狀是(3,1)，$b^{[3]}$的形狀是(1,1)
假設我們存儲的值$n^{[l]}$在一個名爲layers的數組中，如下所示：layer_dims = [$n_x$，4,3,2,1]。因此，第1層有四個隱藏單元，第2層有三個隱藏單元，依此類推。則使用下面的for循環初始化模型的參數：

for(i in range(1, len(layer_dims))):
  parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i-1])) * 0.01
  parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01

該筆記是學習吳恩達老師的課程寫的。初學者入門，如有理解有誤的，歡迎批評指正！

目錄¶

深度學介紹¶

神經網絡基礎¶

淺層神經網絡¶

深度神經網絡¶

相關文章