上溢和下溢¶
- 下溢(underflow)是一種極具毀滅性的舍入誤差.當接近零的數被四捨五入爲零時發生下溢
- 上溢(overflow)是一種極具破壞力的數值錯誤形式.當大量級的數被近似爲\(\infty\)或者\(-\infty\)時發生上溢,進一步的運算通常會導致這些無限值變成非數字.
- softmax 函數(softmax function)可以對上溢和下溢進行數值穩定的一個函數,softmax函數經常用於預測與Multinoulli分佈相關聯的概率,定義爲:
基於梯度的優化方法¶
大多數深度學習算法都涉及某種形式的優化.優化指的是改變\(x\)以最小化或最大化某個函數\(f(x)\)的任務.我們通常以最小化\(f(x)\)指代大多數最優化問題,最大化可以經由最小化算法最小化\(-f(x)\)來實現
我們把要最小化或最大化的函數稱爲目標函數(objective function)或者準則(criterion).當我們對其進行最小化時,也把它稱爲代價函數(cost function),損失函數(loss function)或者誤差函數(error function)
導數¶
導數(derivative):設函數\(y=f(x)\)在點\(x_0\)的某鄰域\(U(x_0)\)內有定義,當自變量\(x\)在點\(x_0\)處取得增量\(\triangle x\)(\(\triangle x \neq 0\) 且\(x_0+\triangle x \in U(x_0)\))時,相應的函數\(y\)取得增量:
\(\(\triangle y = f(x_0 + \triangle x)-f(x_0)\tag{1}\)\)
若極限
\(\(\lim_{\triangle x \rightarrow0}\frac{\triangle y}{\triangle x} = \lim_{\triangle x \rightarrow0}\frac{f(x_0 + \triangle x)-f(x_0)}{\triangle x}\tag{2}\)\)
存在,則稱函數\(y=f(x)\)在點\(x_0\)可導,並稱此極限值爲函數\(y=f(x)\)在點\(x_0\)的導數,記作\(f^\prime(x_0)\)或者\(\left.\frac{dy}{dx}\right | _{x=x_0}\)
由上面的定義可得若曲線\(y=f(x)\)存在一點\((x_0,y_0)\),並且在這點上可導,導數爲\(f^\prime(x_0)\),那麼導數\(f^\prime(x_0)\)就是該點的斜率.
梯度下降(gradient descent)導數對最小化一個函數很有用,當\(\triangle x\)足夠小時,\(f(x-\triangle x{\rm sign}(f^\prime(x)))\)是比\(f(x)\)小的,因此我們可以將\(x\)往導數的反方向移動一小步來減小\(f(x)\).這種技術稱爲梯度下降
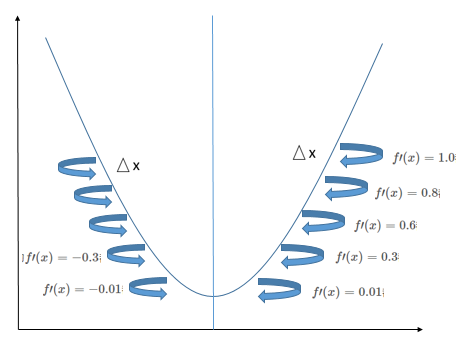
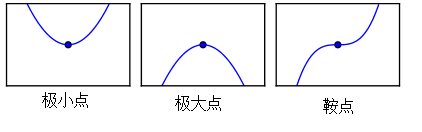
在不斷重複上面操作後,最終可以得到\(f^\prime(x)=0\),改點稱爲臨界點(critical point)或駐點(stationary),這個駐點可能是極大點(maximum),或者是極小點(minimum),還有可能是鞍點(saddle point),還要進一步計算.
- 當駐點的左邊的\(\triangle x\)距離的\(f^\prime(x)\)小於0,而駐點的右邊邊的\(\triangle x\)距離的\(f^\prime(x)\)大於0,則該駐點是極小值
- 當駐點的左邊的\(\triangle x\)距離的\(f^\prime(x)\)大於0,而駐點的右邊邊的\(\triangle x\)距離的\(f^\prime(x)\)小於0,則該駐點是極大值
- 當駐點的距離左右兩邊的\(\triangle x\)距離的\(f^\prime(x)=\)都小於0或都大於0,則該駐點是鞍點
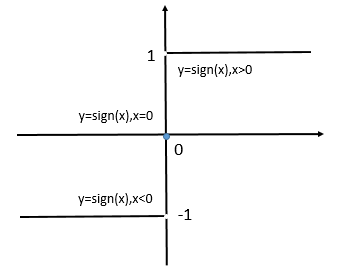
在上面用到了\({\rm sign}\)函數,下面的就是\({\rm sign}\)定義:
\(\({\rm sign}(x) = \left\{ \begin{matrix} 1,x>0 \\\ 0,x=0 \\\ -1,x<0 \end{matrix}\right. \tag{3}\)\)
\({\rm sign}\)函數的座標圖:
偏導數¶
當函數只有二維輸入時,其只有一個駐點,所以這個駐點就是它的最小點或者最大點。但是通常遇到更多的是多維輸入的函數,它具有多個駐點,所以它有多個極小點和極大點,如下圖。所以通過上面的方法很難找到最大點或者最小點。
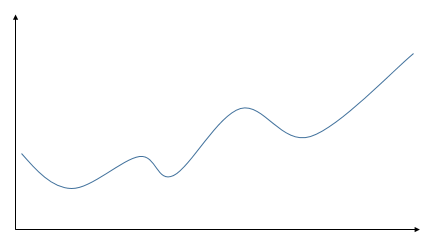
針對具有多維輸入的函數,我們就需要用到偏導數(partial derivative)的概念了。
設函數\(z=f(x,y)\)在點\((x_0,y_0)\)的某個領域內有定義,當\(y\)固定在\(y_0\)而\(x\)在\(x_0\)處有增量\(\triangle x\)時,相應地函數有增量
\(\(f(x_0+\triangle x,y_0)-f(x_0,y_0)\tag{4}\)\)
如果有極限
\(\(\lim_{\triangle x \rightarrow 0}\frac{f(x_0+\triangle x,y_0)-f(x_0,y_0)}{\triangle x}\tag{5}\)\)
存在,則稱此極限爲函數\(z=f(x,y)\)在點\((x_0,y_0)\)處對\(x\)的偏導數,記作:
\(\(\left.\frac{\partial f}{\partial x}\right|_{x=x_0,y=y0}\quad 或\quad f^\prime_x(x_0,y_0)\tag{6}\)\)
同理,函數\(z=f(x,y)\)在點\((x_0,y_0)\)處對\(y\)的偏導數 爲:
例求\(f(x,y)=x^2+3xy+y^2\)在點(2,1)處的偏導數\(f_x(2,1),f_y(2,1)\).
解:把\(y\)看作常數,對\(x\)求導得到
\(\(f_x(x,y)=2x+3y\tag{8}\)\)
把\(x\)看作常數,對\(y\)求導得到
\(\(f_y(x,y)=3x-2y\tag{9}\)\)
代入\(x=2,y=1\),故所求偏導數爲:
\(\(f_x(2,1) = 7,f_y(2,1)=4\tag{10}\)\)
梯度(gradient)是相對一個向量求導的導數:\(f\)的導數是包含所有偏導數的向量,記作\(\nabla_xf(x)\)。梯度的第\(i\)個元素是\(f\)關於\(x_i\)的偏導數。在多維情況下,臨界點是梯度中所有元素都爲零的點。
約束優化¶
有時候,在\(x\)的所有可能值下最大化或者最小化一個函數\(f(x)\)不是我們所希望的,相反,我們可能希望在\(x\)的某些集合\({\Bbb S}\)中找到\(f(x)\)的最大值或者最小值,這個稱爲約束優化(constrained optimization)
Karush-Kuhu-Tucker(KKT)方法是針對約束優化非常通用的解決方案,KKT方法是Lagrange乘子法(只允許等式約束)的推廣
參考資料¶
- lan Goodfellow,Yoshua Bengio,Aaron Courville.深度學習(中文版).趙申劍,黎彧君,符天凡,李凱,譯.北京:人民郵電出版社
- 郭遊瑞,徐應祥,任阿娟,趙志琴.高等數學簡明教程.上海:復旦大學出版社