隨機變量¶
隨機變量(random variable)是可以隨機地取不同值的變量.隨機變量是可以離散的或者連續的,離散隨機變量擁有有限或可數無限多的狀態,連續隨機變量伴隨這實數值的.
概率分佈¶
概率分佈(probability distribution)用來描述隨機變量或一簇隨機變量在每一個可能取到的狀態的可能性大小.
概率質量函數(probability mass function,PMF):離散型變量的概率分佈可以用概率質量函數來描述,通常使用\(P\)表示概率質量函數
概率質量函數可以同時作用於多個隨機變量.這種多個變量的概率分佈被稱爲聯合概率分佈(joint probability distribution).\(P({\bf x}=x,{\bf y}=y)\)表示\({\bf x}=x\)和\({\bf y}=y\)同時發生的概率
一個函數\(P\)是隨機變量\(x\)的PMF,必須滿足以下條件:
1. \(P\)的定義域必須是\(x\)所有可能狀態的集合
2. \(\forall x \in {\bf x},0 \leq P(x) \leq 1\) 不可能發生的事件概率爲0,一定發生的事件概率爲1
3. \(\sum _{x \in {\bf x}}P(x) = 1\)這條性質稱爲歸一化(normalized)
如果一個離散型隨機變量\({\bf x}\)有\(k\)不同的狀態,如果每個每個狀態的可能性都是相同的(均勻分佈(uniform distribution)),那它的PMF爲:
\(\(P({\bf x}=x_i) = \frac{1}{k}\tag{1}\)\)
因爲\(k\)是一個正整數,所以\(\frac {1}{k}\)也是正的,通過下列計算:
\(\(\sum _i P({\bf x}=x_i) = \sum _i \frac{1}{k} = \frac{k}{k} = 1\tag{2}\)\)
所以均勻分佈也是滿足歸一化條件的
邊緣概率¶
邊緣概率分佈(marginal probability distribution):如果我們知道了一組變量的聯合概率分佈,但想要了解其中一個子集的概率分佈,這個子集的概率分佈稱爲邊緣概率分佈
條件概率¶
條件概率:在其他事件發生的條件想該事件發生的概率.計算公式如下\(P({\rm x}=x) > 0\):
\(\(P({\rm x}=x | {\rm y}=y) = \frac{P({\rm x}=x,{\rm y}=y)}{P({\rm x}=x)}\tag{3}\)\)
例題
在一汽車工廠中,一輛汽車有兩道工序是由機器人完成的,其一是緊固3只螺栓,其二是焊接2處焊點。以\(X\)表示由機器人緊固的螺栓緊固得不良的數目,以\(Y\)表示由機器人焊接的不良焊點數目。據積累的資料知\((X,Y)\)具有分佈律:
| Y\X| 0|1|2|3| P{Y=j}|
| :—: |:—:| :—:| :—:| :—:| :—:|
| 0 | 0.840|0.030|0.020|0.010 | 0.900|
| 1 | 0.060|0.010|0.008|0.002| 0.080|
| 2 | 0.010|0.005|0.004|0.001 | 0.020|
| P{X=i} | 0.910|0.045|0.032|0.013 | 1.000|
求在\(X=1\)的條件下,\(Y\)的條件分佈律
\(\(P\{Y=0|X=1\}=\frac{P\{X=1,Y=0\}}{P\{X=1\}}=\frac{0.030}{0.045}\)\)
\(\(P\{Y=1|X=1\}=\frac{P\{X=1,Y=1\}}{P\{X=1\}}=\frac{0.010}{0.045}\tag{4}\)\)
\(\(P\{Y=2|X=1\}=\frac{P\{X=1,Y=2\}}{P\{X=1\}}=\frac{0.005}{0.045}\)\)
獨立性和條件獨立性¶
相互獨立(independent):兩個隨機變量x和y,如果他們的概率分佈可以表示成兩個因子的乘積形式,並且一個因子只包含x,另一個因子只包含y,我們就能稱這兩隨機變量是相互獨立的.計算如下:
\(\(\forall x \in {\rm x},y \in {\rm y},p({\rm x} = x,{\rm y} = y)=p({\rm x} = x)p({\rm y} = y\tag{5})\)\)
例題
實驗\(E\)爲“拋甲、乙兩枚硬幣,觀察正(H)反(T)面出現的情況”。設事件\(A\)爲“甲幣出現H”,事件B爲“乙幣出現H”。\(E\)的樣本空間:
\(\(S=\{HH,HT,TH,TT\}\tag{6}\)\)
即:
\(\(P(A)=\frac{2}{4}=\frac{1}{2},P(B)=\frac{2}{4}=\frac{1}{2} \\
P(B|A)=\frac{1}{2},P(AB)=\frac{1}{4}\tag{7}\)\)
由上可得\(P(B|A)=P(B)\),而\(P(AB)=P(A)P(B)\)。所以我們知道甲幣是否出現正面與乙幣是否出現正面是互不影響的。
條件獨立(conditionally independent):如果關於x和y的條件概率分佈對於\(z\)的每一個值都可以寫成乘積的形式那麼這兩個隨機變量x和y子在給定隨機變量\(z\)時是條件獨立的,計算如下:
\(\(\forall x \in {\rm x},y \in {\rm y},z \in {\rm z},p({\rm x} = x,{\rm y} = y | {\rm z} = z)=p({\rm x } = x | {\rm z} = z)p({\rm y} = y | {\rm z} = z)\tag{8}\)\)
數學期望¶
設離散型隨機變量\(X\)的分佈律如下:
\(\(P\{X=x_k\}=p_x,k=1,2,3,\ldots\tag{9}\)\)
若是級數絕對收斂,則稱級數\(\sum_{k=1}^\infty x_k p_k\)的和爲隨機變量\(X\)的數學期望,記作\(E(X)\),公式如下:
\(\(E(X)=\sum_{k=1}^\infty x_k p_k\tag{10}\)\)
設連續型隨機變量\(X\)的概率密度爲\(f(x)\),若爲積分絕對收斂,則稱積分\(\int_{-\infty}^\infty xf(x)dx\)的值爲隨機變量\(X\)的數學期望,記作\(E(X)\),公式如下:
\(\(E(X)=\int_{-\infty}^\infty xf(x)dx\tag{11}\)\)
數學期望簡稱期望,又稱均值.
數學期望\(E(X)\)完全由隨機變量\(X\)的概率分佈所確定的,若\(X\)從某一分佈,也稱爲\(E(X)\)是這一分佈的數學期望
離散型例題
某醫院當新生兒誕生時,醫生要根據嬰兒的皮膚顏色、肌肉彈性、反應的敏感性、心臟的搏動等方面的情況進行評分,新生兒的得分\(X\)是一個隨機變量,根據以往資料表明\(X\)的分佈律爲:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(p_k\) | 0.002 | 0.001 | 0.002 | 0.005 | 0.02 | 0.04 | 0.18 | 0.37 | 0.25 | 0.12 | 0.01 |
求\(X\)的數學期望\(E(X)\)
\(\(E(X)=0\times0.002+1\times0.001+2\times0.002+3\times0.005+4\times0.02+\\ 5\times0.04+6\times0.18+7\times0.37+8\times0.25+9\times0.12+10\times0.01=7.15\)\)
連續型例題
有兩個相互獨立工作的電子裝置,它們的壽命(以小時計)\(X_k=(k=1,2)\)服從同一指數分佈,其概率密度爲:
\(\(f(x)=\left\{\begin{matrix}\frac{1}{\theta}e^{-x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right., \quad \theta > 0\tag{12}\)\)
若將這兩個電子裝置串聯連接組成整機,求整機壽命(以小時計)\(N\)的數學期望。
解:\(X_k(k=1,2)\)的分佈函數爲:
\(\(F(x)=\left\{\begin{matrix}1-e^{-x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right.\tag{12}\)\)
由\(N=\min\{X_1,X_2\}\)的分佈函數
\(\(F_{\min}(x)=1-[1-F(x)]^2=\left\{\begin{matrix}1-e^{-2x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right.\tag{13}\)\)
因而\(N\)的概率密度爲:
\(\(f_{\min}(x)=\left\{\begin{matrix}\frac{2}{\theta}e^{-2x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right.\tag{14}\)\)
於是\(N\)的數學期望爲:
\(\(E(N)=\int_{-\infty} ^\infty xf_\min(x)dx=\int_0^\infty\frac{2x}{\theta}e^{-2x/\theta}dx=\frac{\theta}{2}\tag{15}\)\)
方差¶
方差(variance)設\(X\)是一個隨機變量,若\(E\{[X-E(X)]^2\}\)存在,則稱\(E\{[X-E(X)]^2\}\)爲\(X\)的方差,記爲\(D(X)\)或\(Var(X)\),即:
\(\(D(X)=Var(X)=E\{[X-E(X)]^2\}\tag{16}\)\)
如果方差很小是,\(X\)的值形成的簇比較接近它們的數學期望.方差的平方根\(\sqrt{D(X)}\)稱爲標準差(standard deviation)或均方差(mean square deviation)
當\(X\)爲離散型隨機變量時:
\(\(D(X)=\sum_{k=1}^\infty[x_k-E(X)]^2p_k\tag{17}\)\)
當\(X\)爲連續型隨機變量時:
\(\(D(X)=\int_{-\infty}^\infty[x-E(X)]^2f(x)dx\tag{18}\)\)
協方差¶
量\(E\{[X-E(X)][Y-E(Y)]\}\)稱爲隨機變量X與Y的協方差(covariance),記作\(Cov(X,Y)\),公式如下:
\(\(Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}\tag{19}\)\)
而
\(\(\rho_{xy}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\tag{20}\)\)
稱爲隨機變量\(X\)和\(Y\)的相關係數(correlation)
協方差矩陣¶
二維隨機變量\((X_1,X_2)\)有四個二階中心矩(設它們都存在),分別記爲:
$$
c_{11} = E{[X_1-E(X_1)]^2} \\c_{12} = E{[X_1-E(X_1)][X_2-E(X_2)]} \\c_{21} = E{[X_2-E(X_2)][X_1-E(X_1)]} \\c_{22} = E{[X_2-E(X_2)]^2} \tag{21}$$
將它們排列成矩陣的形式:
$$
\left(
\begin{matrix}
c_{11} & c_{12} \
c_{21} & c_{22}
\end{matrix}
\right) \tag{22}
$$
這個矩陣稱爲隨機變量\((X_1,X_2)\)的協方差矩陣(covariance matrix)
常用的概率分佈¶
Bernoulli 分佈¶
Bernoulli 分佈(Bernoulli distribution)是單個二值隨機變量的分佈,它由單個參\(\phi \in [0,1]\)控制,\(\phi\)給出了隨機變量等於1的概率.
Multinoulli 分佈¶
Multinoulli 分佈(multinoulli distribution)或者範疇分佈(categorical distribution)是指在具有\(k\)個不同狀態的單個離散隨機變量上的分佈,其中\(k\)是一個有限值.
高斯分佈¶
高斯分佈(Gaussian distribution)也叫正態分佈(normal distribution):
\(\({\cal N}(x;\mu,\sigma^2)=\sqrt{\frac{1}{2\pi \sigma^2}}{\rm exp}(-\frac{1}{2\sigma^2}(x-\mu)^2)\tag{23}\)\)
當\(\mu=0,\sigma=1\)是,這個我們稱爲標準正態分佈(standard normal distribution)
常用函數¶
logistic sigmoid函數¶
公式:
\(\(\sigma(x)=\frac{1}{1+{\rm exp}(-x)}\tag{24}\)\)
logistic sigmoid函數圖
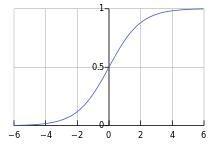
*圖片來自網絡
softplus 函數¶
公式:
\(\(\varsigma(x)=\log(1+\exp(x))\tag{25}\)\)
softplus函數名來源於它是另一個函數的平滑(或”軟化”)形式,這個函數是:
\(\(x^+=\max(0,x)\)\)
softplus函數的圖
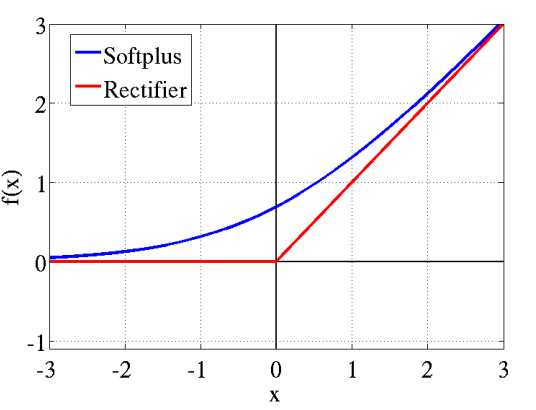
*圖片來自網絡
參考資料¶
- lan Goodfellow,Yoshua Bengio,Aaron Courville.深度學習(中文版).趙申劍,黎彧君,符天凡,李凱,譯.北京:人民郵電出版社
- 浙江大學,盛驟,謝式千,潘承毅.工程數學-概率論與數理統計(第四版).北京:高等教育出版社