随机变量¶
随机变量(random variable)是可以随机地取不同值的变量.随机变量是可以离散的或者连续的,离散随机变量拥有有限或可数无限多的状态,连续随机变量伴随这实数值的.
概率分布¶
概率分布(probability distribution)用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小.
概率质量函数(probability mass function,PMF):离散型变量的概率分布可以用概率质量函数来描述,通常使用\(P\)表示概率质量函数
概率质量函数可以同时作用于多个随机变量.这种多个变量的概率分布被称为联合概率分布(joint probability distribution).\(P({\bf x}=x,{\bf y}=y)\)表示\({\bf x}=x\)和\({\bf y}=y\)同时发生的概率
一个函数\(P\)是随机变量\(x\)的PMF,必须满足以下条件:
1. \(P\)的定义域必须是\(x\)所有可能状态的集合
2. \(\forall x \in {\bf x},0 \leq P(x) \leq 1\) 不可能发生的事件概率为0,一定发生的事件概率为1
3. \(\sum _{x \in {\bf x}}P(x) = 1\)这条性质称为归一化(normalized)
如果一个离散型随机变量\({\bf x}\)有\(k\)不同的状态,如果每个每个状态的可能性都是相同的(均匀分布(uniform distribution)),那它的PMF为:
\(\(P({\bf x}=x_i) = \frac{1}{k}\tag{1}\)\)
因为\(k\)是一个正整数,所以\(\frac {1}{k}\)也是正的,通过下列计算:
\(\(\sum _i P({\bf x}=x_i) = \sum _i \frac{1}{k} = \frac{k}{k} = 1\tag{2}\)\)
所以均匀分布也是满足归一化条件的
边缘概率¶
边缘概率分布(marginal probability distribution):如果我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布,这个子集的概率分布称为边缘概率分布
条件概率¶
条件概率:在其他事件发生的条件想该事件发生的概率.计算公式如下\(P({\rm x}=x) > 0\):
\(\(P({\rm x}=x | {\rm y}=y) = \frac{P({\rm x}=x,{\rm y}=y)}{P({\rm x}=x)}\tag{3}\)\)
例题
在一汽车工厂中,一辆汽车有两道工序是由机器人完成的,其一是紧固3只螺栓,其二是焊接2处焊点。以\(X\)表示由机器人紧固的螺栓紧固得不良的数目,以\(Y\)表示由机器人焊接的不良焊点数目。据积累的资料知\((X,Y)\)具有分布律:
| Y\X| 0|1|2|3| P{Y=j}|
| :—: |:—:| :—:| :—:| :—:| :—:|
| 0 | 0.840|0.030|0.020|0.010 | 0.900|
| 1 | 0.060|0.010|0.008|0.002| 0.080|
| 2 | 0.010|0.005|0.004|0.001 | 0.020|
| P{X=i} | 0.910|0.045|0.032|0.013 | 1.000|
求在\(X=1\)的条件下,\(Y\)的条件分布律
\(\(P\{Y=0|X=1\}=\frac{P\{X=1,Y=0\}}{P\{X=1\}}=\frac{0.030}{0.045}\)\)
\(\(P\{Y=1|X=1\}=\frac{P\{X=1,Y=1\}}{P\{X=1\}}=\frac{0.010}{0.045}\tag{4}\)\)
\(\(P\{Y=2|X=1\}=\frac{P\{X=1,Y=2\}}{P\{X=1\}}=\frac{0.005}{0.045}\)\)
独立性和条件独立性¶
相互独立(independent):两个随机变量x和y,如果他们的概率分布可以表示成两个因子的乘积形式,并且一个因子只包含x,另一个因子只包含y,我们就能称这两随机变量是相互独立的.计算如下:
\(\(\forall x \in {\rm x},y \in {\rm y},p({\rm x} = x,{\rm y} = y)=p({\rm x} = x)p({\rm y} = y\tag{5})\)\)
例题
实验\(E\)为“抛甲、乙两枚硬币,观察正(H)反(T)面出现的情况”。设事件\(A\)为“甲币出现H”,事件B为“乙币出现H”。\(E\)的样本空间:
\(\(S=\{HH,HT,TH,TT\}\tag{6}\)\)
即:
\(\(P(A)=\frac{2}{4}=\frac{1}{2},P(B)=\frac{2}{4}=\frac{1}{2} \\
P(B|A)=\frac{1}{2},P(AB)=\frac{1}{4}\tag{7}\)\)
由上可得\(P(B|A)=P(B)\),而\(P(AB)=P(A)P(B)\)。所以我们知道甲币是否出现正面与乙币是否出现正面是互不影响的。
条件独立(conditionally independent):如果关于x和y的条件概率分布对于\(z\)的每一个值都可以写成乘积的形式那么这两个随机变量x和y子在给定随机变量\(z\)时是条件独立的,计算如下:
\(\(\forall x \in {\rm x},y \in {\rm y},z \in {\rm z},p({\rm x} = x,{\rm y} = y | {\rm z} = z)=p({\rm x } = x | {\rm z} = z)p({\rm y} = y | {\rm z} = z)\tag{8}\)\)
数学期望¶
设离散型随机变量\(X\)的分布律如下:
\(\(P\{X=x_k\}=p_x,k=1,2,3,\ldots\tag{9}\)\)
若是级数绝对收敛,则称级数\(\sum_{k=1}^\infty x_k p_k\)的和为随机变量\(X\)的数学期望,记作\(E(X)\),公式如下:
\(\(E(X)=\sum_{k=1}^\infty x_k p_k\tag{10}\)\)
设连续型随机变量\(X\)的概率密度为\(f(x)\),若为积分绝对收敛,则称积分\(\int_{-\infty}^\infty xf(x)dx\)的值为随机变量\(X\)的数学期望,记作\(E(X)\),公式如下:
\(\(E(X)=\int_{-\infty}^\infty xf(x)dx\tag{11}\)\)
数学期望简称期望,又称均值.
数学期望\(E(X)\)完全由随机变量\(X\)的概率分布所确定的,若\(X\)从某一分布,也称为\(E(X)\)是这一分布的数学期望
离散型例题
某医院当新生儿诞生时,医生要根据婴儿的皮肤颜色、肌肉弹性、反应的敏感性、心脏的搏动等方面的情况进行评分,新生儿的得分\(X\)是一个随机变量,根据以往资料表明\(X\)的分布律为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(p_k\) | 0.002 | 0.001 | 0.002 | 0.005 | 0.02 | 0.04 | 0.18 | 0.37 | 0.25 | 0.12 | 0.01 |
求\(X\)的数学期望\(E(X)\)
\(\(E(X)=0\times0.002+1\times0.001+2\times0.002+3\times0.005+4\times0.02+\\ 5\times0.04+6\times0.18+7\times0.37+8\times0.25+9\times0.12+10\times0.01=7.15\)\)
连续型例题
有两个相互独立工作的电子装置,它们的寿命(以小时计)\(X_k=(k=1,2)\)服从同一指数分布,其概率密度为:
\(\(f(x)=\left\{\begin{matrix}\frac{1}{\theta}e^{-x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right., \quad \theta > 0\tag{12}\)\)
若将这两个电子装置串联连接组成整机,求整机寿命(以小时计)\(N\)的数学期望。
解:\(X_k(k=1,2)\)的分布函数为:
\(\(F(x)=\left\{\begin{matrix}1-e^{-x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right.\tag{12}\)\)
由\(N=\min\{X_1,X_2\}\)的分布函数
\(\(F_{\min}(x)=1-[1-F(x)]^2=\left\{\begin{matrix}1-e^{-2x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right.\tag{13}\)\)
因而\(N\)的概率密度为:
\(\(f_{\min}(x)=\left\{\begin{matrix}\frac{2}{\theta}e^{-2x/\theta},& x > 0 \\ 0,& x \leq0\end{matrix}\right.\tag{14}\)\)
于是\(N\)的数学期望为:
\(\(E(N)=\int_{-\infty} ^\infty xf_\min(x)dx=\int_0^\infty\frac{2x}{\theta}e^{-2x/\theta}dx=\frac{\theta}{2}\tag{15}\)\)
方差¶
方差(variance)设\(X\)是一个随机变量,若\(E\{[X-E(X)]^2\}\)存在,则称\(E\{[X-E(X)]^2\}\)为\(X\)的方差,记为\(D(X)\)或\(Var(X)\),即:
\(\(D(X)=Var(X)=E\{[X-E(X)]^2\}\tag{16}\)\)
如果方差很小是,\(X\)的值形成的簇比较接近它们的数学期望.方差的平方根\(\sqrt{D(X)}\)称为标准差(standard deviation)或均方差(mean square deviation)
当\(X\)为离散型随机变量时:
\(\(D(X)=\sum_{k=1}^\infty[x_k-E(X)]^2p_k\tag{17}\)\)
当\(X\)为连续型随机变量时:
\(\(D(X)=\int_{-\infty}^\infty[x-E(X)]^2f(x)dx\tag{18}\)\)
协方差¶
量\(E\{[X-E(X)][Y-E(Y)]\}\)称为随机变量X与Y的协方差(covariance),记作\(Cov(X,Y)\),公式如下:
\(\(Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}\tag{19}\)\)
而
\(\(\rho_{xy}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\tag{20}\)\)
称为随机变量\(X\)和\(Y\)的相关系数(correlation)
协方差矩阵¶
二维随机变量\((X_1,X_2)\)有四个二阶中心矩(设它们都存在),分别记为:
$$
c_{11} = E{[X_1-E(X_1)]^2} \\c_{12} = E{[X_1-E(X_1)][X_2-E(X_2)]} \\c_{21} = E{[X_2-E(X_2)][X_1-E(X_1)]} \\c_{22} = E{[X_2-E(X_2)]^2} \tag{21}$$
将它们排列成矩阵的形式:
$$
\left(
\begin{matrix}
c_{11} & c_{12} \
c_{21} & c_{22}
\end{matrix}
\right) \tag{22}
$$
这个矩阵称为随机变量\((X_1,X_2)\)的协方差矩阵(covariance matrix)
常用的概率分布¶
Bernoulli 分布¶
Bernoulli 分布(Bernoulli distribution)是单个二值随机变量的分布,它由单个参\(\phi \in [0,1]\)控制,\(\phi\)给出了随机变量等于1的概率.
Multinoulli 分布¶
Multinoulli 分布(multinoulli distribution)或者范畴分布(categorical distribution)是指在具有\(k\)个不同状态的单个离散随机变量上的分布,其中\(k\)是一个有限值.
高斯分布¶
高斯分布(Gaussian distribution)也叫正态分布(normal distribution):
\(\({\cal N}(x;\mu,\sigma^2)=\sqrt{\frac{1}{2\pi \sigma^2}}{\rm exp}(-\frac{1}{2\sigma^2}(x-\mu)^2)\tag{23}\)\)
当\(\mu=0,\sigma=1\)是,这个我们称为标准正态分布(standard normal distribution)
常用函数¶
logistic sigmoid函数¶
公式:
\(\(\sigma(x)=\frac{1}{1+{\rm exp}(-x)}\tag{24}\)\)
logistic sigmoid函数图
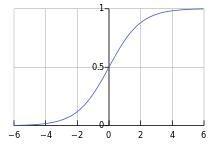
*图片来自网络
softplus 函数¶
公式:
\(\(\varsigma(x)=\log(1+\exp(x))\tag{25}\)\)
softplus函数名来源于它是另一个函数的平滑(或”软化”)形式,这个函数是:
\(\(x^+=\max(0,x)\)\)
softplus函数的图
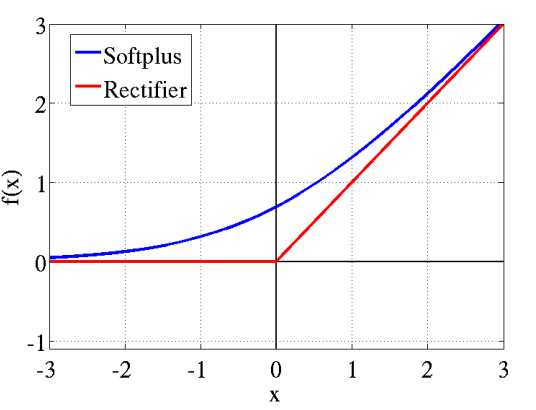
*图片来自网络
参考资料¶
- lan Goodfellow,Yoshua Bengio,Aaron Courville.深度学习(中文版).赵申剑,黎彧君,符天凡,李凯,译.北京:人民邮电出版社
- 浙江大学,盛骤,谢式千,潘承毅.工程数学-概率论与数理统计(第四版).北京:高等教育出版社