Overflow and Underflow¶
- Underflow is a devastating form of rounding error that occurs when numbers close to zero are rounded to zero.
- Overflow is a destructive numerical error that occurs when numbers of large magnitude are approximated as \(\infty\) or \(-\infty\). Further operations typically lead these infinite values to become non-numeric.
- The softmax function is a numerically stable function for handling overflow and underflow. It is commonly used to predict probabilities associated with Multinoulli distributions. Its definition is:
Gradient-Based Optimization Methods¶
Most deep learning algorithms involve some form of optimization. Optimization refers to the task of changing \(x\) to minimize or maximize a function \(f(x)\). We typically refer to minimizing \(f(x)\) for most optimization problems, while maximizing can be achieved by minimizing \(-f(x)\).
The function we aim to minimize or maximize is called the objective function or criterion. When minimizing, it is also referred to as the cost function, loss function, or error function.
Derivatives¶
Derivative: Let the function \(y = f(x)\) be defined in a neighborhood \(U(x_0)\) of point \(x_0\). When the independent variable \(x\) takes an increment \(\triangle x\) (where \(\triangle x \neq 0\) and \(x_0 + \triangle x \in U(x_0)\)), the corresponding function \(y\) takes an increment:
\(\(\triangle y = f(x_0 + \triangle x) - f(x_0) \tag{1}\)\)
If the limit
\(\(\lim_{\triangle x \rightarrow 0} \frac{\triangle y}{\triangle x} = \lim_{\triangle x \rightarrow 0} \frac{f(x_0 + \triangle x) - f(x_0)}{\triangle x} \tag{2}\)\)
exists, the function \(y = f(x)\) is said to be differentiable at point \(x_0\), and this limit value is called the derivative of \(y = f(x)\) at \(x_0\), denoted as \(f^\prime(x_0)\) or \(\left. \frac{dy}{dx} \right|_{x=x_0}\).
From the above definition, if the curve \(y = f(x)\) has a point \((x_0, y_0)\) and is differentiable at this point with derivative \(f^\prime(x_0)\), then \(f^\prime(x_0)\) is the slope of the curve at this point.
Gradient Descent is useful for minimizing a function using derivatives. When \(\triangle x\) is sufficiently small, \(f(x - \triangle x \cdot \text{sign}(f^\prime(x)))\) is smaller than \(f(x)\). Thus, we can move \(x\) a small step in the direction opposite to the derivative to reduce \(f(x)\). This technique is called gradient descent.
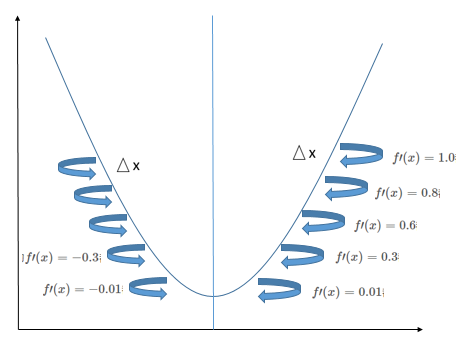
After repeatedly performing the above operation, we eventually get \(f^\prime(x) = 0\). This point is called a critical point or stationary point. This stationary point could be a maximum, a minimum, or a saddle point, which requires further analysis:
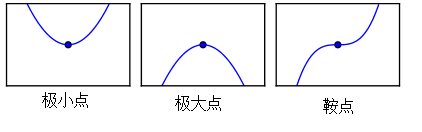
- If for a stationary point, \(f^\prime(x)\) is negative for \(\triangle x\) to the left and positive for \(\triangle x\) to the right, the point is a minimum.
- If \(f^\prime(x)\) is positive for \(\triangle x\) to the left and negative for \(\triangle x\) to the right, the point is a maximum.
- If \(f^\prime(x)\) is both negative or both positive for \(\triangle x\) on both sides, the point is a saddle point.
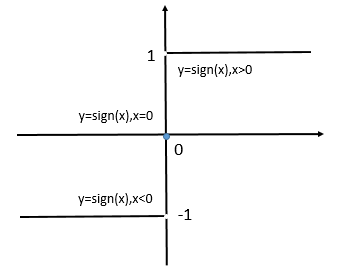
The \(\text{sign}\) function is used above, with the definition:
\(\(\text{sign}(x) = \begin{cases}
1, & x > 0 \\
0, & x = 0 \\
-1, & x < 0
\end{cases} \tag{3}\)\)
The graph of the \(\text{sign}\) function:
Partial Derivatives¶
When a function has only two-dimensional inputs, it has only one stationary point, which is either its minimum or maximum. However, we often encounter functions with multi-dimensional inputs, which can have multiple stationary points (minima and maxima), as shown in the figure below. Thus, the previous method is insufficient to find these extrema.
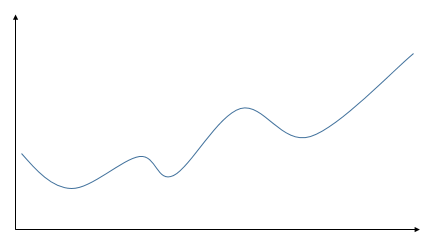
For functions with multi-dimensional inputs, we need the concept of partial derivatives.
Let the function \(z = f(x, y)\) be defined in a neighborhood around \((x_0, y_0)\). When \(y\) is fixed at \(y_0\) and \(x\) takes an increment \(\triangle x\) at \(x_0\), the corresponding function increment is:
\(\(f(x_0 + \triangle x, y_0) - f(x_0, y_0) \tag{4}\)\)
If the limit
\(\(\lim_{\triangle x \rightarrow 0} \frac{f(x_0 + \triangle x, y_0) - f(x_0, y_0)}{\triangle x} \tag{5}\)\)
exists, this limit is called the partial derivative of \(z = f(x, y)\) with respect to \(x\) at \((x_0, y_0)\), denoted as:
\(\(\left. \frac{\partial f}{\partial x} \right|_{x=x_0, y=y_0} \quad \text{or} \quad f^\prime_x(x_0, y_0) \tag{6}\)\)
Similarly, the partial derivative of \(z = f(x, y)\) with respect to \(y\) at \((x_0, y_0)\) is:
\(\(f^\prime_y(x_0, y_0) = \lim_{\triangle y \rightarrow 0} \frac{f(x_0, y_0 + \triangle y) - f(x_0, y_0)}{\triangle y} \tag{7}\)\)
Example: Find the partial derivatives \(f_x(2, 1)\) and \(f_y(2, 1)\) of \(f(x, y) = x^2 + 3xy + y^2\) at the point \((2, 1)\).
Solution: Treat \(y\) as a constant and differentiate with respect to \(x\):
\(\(f_x(x, y) = 2x + 3y \tag{8}\)\)
Treat \(x\) as a constant and differentiate with respect to \(y\):
\(\(f_y(x, y) = 3x + 2y \tag{9}\)\)
Substitute \(x = 2\) and \(y = 1\):
\(\(f_x(2, 1) = 7, \quad f_y(2, 1) = 8 \tag{10}\)\)
Gradient is the derivative of a function with respect to a vector. The gradient of \(f\), denoted \(\nabla_x f(x)\), is a vector containing all partial derivatives. The \(i\)-th element of the gradient is the partial derivative of \(f\) with respect to \(x_i\). In multi-dimensional cases, a critical point is where all elements of the gradient are zero.
Constrained Optimization¶
Sometimes, maximizing or minimizing a function \(f(x)\) over all possible values of \(x\) is not desired. Instead, we may need to find the maximum or minimum of \(f(x)\) within a specific set \(\mathbb{S}\) of possible \(x\) values. This is called constrained optimization.
The Karush-Kuhn-Tucker (KKT) method is a general solution for constrained optimization. KKT is an extension of the Lagrange multiplier method (which only handles equality constraints).
References¶
- Ian Goodfellow, Yoshua Bengio, Aaron Courville. Deep Learning (Chinese Edition). Translated by Shenjian Zhao, Yujun Li, Tianfan Fu, Kai Li. Beijing: Posts & Telecom Press.
- Yourui Guo, Yingxiang Xu, Aijuan Ren, Zhiqin Zhao. A Concise Course in Higher Mathematics. Shanghai: Fudan University Press.