使用带有隐层的神经网络实现颜色二分类

前言
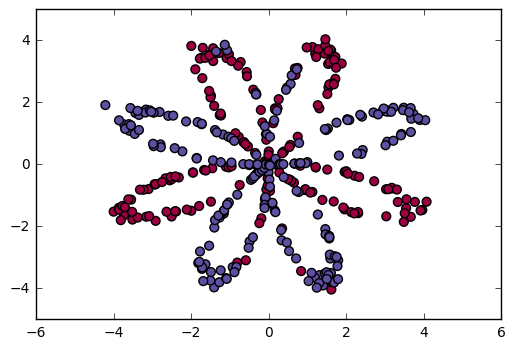
数据集是一个红色和蓝色的的分布。其分布图如下:
导包
导入依赖包,这个两个分别是加载数据的工具函数和数据集,这个两个程序可以在这里下载。这个工具函数中使用到sklearn包,使用之前还要使用pip安装该函数。
from planar_utils import sigmoid, load_planar_dataset
from testCases_v2 import *
加载数据
加载数据和获取数据的形状
# 加载数据
X, Y = load_planar_dataset()
# 获取数据的形状
shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1]
神经网络模型
定义神经网络结构
定义神经网络结构,比如数据的大小,对应的标签和有多少个隐层。
def layer_sizes(X, Y):
"""
定义神经网络结构
:param X: 形状的输入数据集(输入大小,示例数量)
:param Y: 形状标签(输出尺寸,示例数量)
:return:
n_x -- 输入层的大小。
n_h -- 隐藏层的大小。
n_y -- 隐藏层的大小。。
"""
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
return (n_x, n_h, n_y)
初始化模型的参数
根据神经网络的结构来初始化模型权重和偏置值,并把权重和偏置值存放在参数字典中。权重向量使用随机初始化,偏置向量初始化为零矩阵。
def initialize_parameters(n_x, n_h, n_y):
"""
初始化模型的参数
:param n_x: 输入层的大小
:param n_h: 隐藏层的大小
:param n_y: 隐藏层的大小
:return:
params --包含您的参数的python字典:
W1 -- 形状重量矩阵(n_h, n_x)
b1 -- 形状的偏置向量(n_h, 1)
W2 -- 形状重量矩阵(n_y, n_h)
b2 -- 形状的偏置向量(n_y, 1)
"""
np.random.seed(2)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
正向传播
这个正向传播使用了两个激活函数,一个是tanh函数,另一个是sigmoid函数。
def forward_propagation(X, parameters):
"""
向前传播
:param X: 输入数据大小(n_x, m)
:param parameters: 包含参数的python字典(初始化函数的输出)
:return:
A2 -- 第二个激活的sigmoid输出。
cache -- 包含“Z1”、“A1”、“Z2”和“A2”的字典
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
assert (A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
计算损失函数
以下就是要计算的损失函数的公式:
$$
J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{1}
$$
def compute_cost(A2, Y):
"""
计算公式(1)中的交叉熵成本
:param A2: 第二次激活的sigmoid输出,形状(1,示例数量)
:param Y: “真”标签向量的形状(1,样本数目)
:return:
cost -- 交叉熵成本方程(1)
"""
m = Y.shape[1] # number of example
logprobs = np.multiply(np.log(A2), Y) + np.multiply(1 - Y, np.log(1 - A2))
cost = -(np.sum(logprobs)) / m
cost = np.squeeze(cost) # 确保成本是我们期望的尺寸。
assert (isinstance(cost, float))
return cost
反向传播
反向传播使用到了以下这些公式:

def backward_propagation(parameters, cache, X, Y):
"""
使用上面的说明实现反向传播。
:param parameters: 包含我们的参数的python字典。
:param cache: 包含“Z1”、“A1”、“Z2”和“A2”的字典。
:param X: 形状输入数据(2,实例数)
:param Y: “真”标签向量的形状(1,样本数目)
:return:
grads -- 包含不同参数的渐变的python字典
"""
m = X.shape[1]
m = float(m)
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
更新参数
实施更新规则。使用梯度下降。您必须使用(dW1,db1,dW2,db2)才能更新(W1,b1,W2,b2),使用到更新的规则公式如下:
$$
\theta = \theta - \alpha \frac{\partial J }{ \partial \theta }\tag{2}
$$
def update_parameters(parameters, grads, learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数。
:param parameters: 包含参数的python字典。
:param grads: 包含梯度的python字典。
:param learning_rate: 学习率
:return:
parameters -- 包含更新参数的python字典。
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
集成model函数
把上面定义的神经网络结构的函数集成到这个函数中,形成一个完整的神经网络。
def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
"""
把上面定义的神经网络集成到这个函数
:param X: 形状数据集(2,样本数目)
:param Y: 形状标签(1,样本数目)
:param n_h: 隐藏层的大小
:param num_iterations: 梯度下降循环的迭代次数。
:param print_cost: 如果是真的,打印每1000次迭代的成本。
:return:
parameters -- 由模型学习的参数。他们可以被用来预测。
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x, n_h, n_y)
for i in range(0, num_iterations):
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2, Y)
grads = backward_propagation(parameters, cache, X, Y)
parameters = update_parameters(parameters, grads)
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" % (i, cost))
return parameters
预测结果
使用您的模型通过构建predict()来进行预测。使用向前传播来预测结果。
$$
y_{prediction} = \mathbb 1 \text{{activation > 0.5}} = \begin{cases}
1 & \text{if}\ activation > 0.5 \
0 & \text{otherwise}
\end{cases}\tag{3}
$$
def predict(parameters, X):
"""
使用学习的参数,为X中的每个例子预测一个类。
:param parameters: 包含参数的python字典。
:param X: 输入数据大小(n_x, m)
:return:
predictions -- 模型预测向量(红色:0 / blue: 1)
"""
A2, cache = forward_propagation(X, parameters)
predictions = A2 > 0.5
return predictions
测试其他隐层
通过测试不用的隐层数量,观察模型的预测效果,获得最优的隐层数量。
def test_anther_hidden():
"""
使用不同的隐层训练
:return:
"""
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
parameters = nn_model(X, Y, n_h, num_iterations=1000)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
调用函数训练
通过调用刚才集成的神经网络函数nn_model()来训练参数,获得参数之后就可以是参数预测数据了。
if __name__ == "__main__":
parameters = nn_model(X, Y, n_h=4, num_iterations=10000, print_cost=True)
predictions = predict(parameters, X)
print 'Accuracy: %d' % float(
(np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%'
训练和预测输出的结果是:
Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219415
Cost after iteration 9000: 0.218547
Accuracy: 90%
这个使用的是不同的隐层训练和预测
if __name__ == "__main__":
test_anther_hidden()
以下就是不同的隐层训练后得到的不同准确率。
Accuracy for 1 hidden units: 67.75 %
Accuracy for 2 hidden units: 65.25 %
Accuracy for 3 hidden units: 89.5 %
Accuracy for 4 hidden units: 89.25 %
Accuracy for 5 hidden units: 89.5 %
Accuracy for 20 hidden units: 88.0 %
Accuracy for 50 hidden units: 88.0 %
所有代码
为了方便读者阅读代码,这里放出了所有的代码(除了那两个工具类):
# coding=utf-8
from planar_utils import sigmoid, load_planar_dataset
from testCases_v2 import *
# 加载数据
X, Y = load_planar_dataset()
# 获取数据的形状
shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1]
def layer_sizes(X, Y):
"""
定义神经网络结构
:param X: 形状的输入数据集(输入大小,示例数量)
:param Y: 形状标签(输出尺寸,示例数量)
:return:
n_x -- 输入层的大小。
n_h -- 隐藏层的大小。
n_y -- 隐藏层的大小。。
"""
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
return (n_x, n_h, n_y)
def initialize_parameters(n_x, n_h, n_y):
"""
初始化模型的参数
:param n_x: 输入层的大小
:param n_h: 隐藏层的大小
:param n_y: 隐藏层的大小
:return:
params --包含您的参数的python字典:
W1 -- 形状重量矩阵(n_h, n_x)
b1 -- 形状的偏置向量(n_h, 1)
W2 -- 形状重量矩阵(n_y, n_h)
b2 -- 形状的偏置向量(n_y, 1)
"""
np.random.seed(2)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def forward_propagation(X, parameters):
"""
向前传播
:param X: 输入数据大小(n_x, m)
:param parameters: 包含参数的python字典(初始化函数的输出)
:return:
A2 -- 第二个激活的sigmoid输出。
cache -- 包含“Z1”、“A1”、“Z2”和“A2”的字典
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
assert (A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
def compute_cost(A2, Y):
"""
计算公式(13)中的交叉熵成本
:param A2: 第二次激活的sigmoid输出,形状(1,示例数量)
:param Y: “真”标签向量的形状(1,样本数目)
:return:
cost -- 交叉熵成本方程(13)
"""
m = Y.shape[1] # number of example
logprobs = np.multiply(np.log(A2), Y) + np.multiply(1 - Y, np.log(1 - A2))
cost = -(np.sum(logprobs)) / m
cost = np.squeeze(cost) # 确保成本是我们期望的尺寸。
assert (isinstance(cost, float))
return cost
def backward_propagation(parameters, cache, X, Y):
"""
使用上面的说明实现反向传播。
:param parameters: 包含我们的参数的python字典。
:param cache: 包含“Z1”、“A1”、“Z2”和“A2”的字典。
:param X: 形状输入数据(2,实例数)
:param Y: “真”标签向量的形状(1,样本数目)
:return:
grads -- 包含不同参数的渐变的python字典
"""
m = X.shape[1]
m = float(m)
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
def update_parameters(parameters, grads, learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数。
:param parameters: 包含参数的python字典。
:param grads: 包含梯度的python字典。
:param learning_rate: 学习率
:return:
parameters -- 包含更新参数的python字典。
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
"""
把上面定义的神经网络集成到这个函数
:param X: 形状数据集(2,样本数目)
:param Y: 形状标签(1,样本数目)
:param n_h: 隐藏层的大小
:param num_iterations: 梯度下降循环的迭代次数。
:param print_cost: 如果是真的,打印每1000次迭代的成本。
:return:
parameters -- 由模型学习的参数。他们可以被用来预测。
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x, n_h, n_y)
for i in range(0, num_iterations):
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2, Y)
grads = backward_propagation(parameters, cache, X, Y)
parameters = update_parameters(parameters, grads)
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" % (i, cost))
return parameters
def predict(parameters, X):
"""
使用学习的参数,为X中的每个例子预测一个类。
:param parameters: 包含参数的python字典。
:param X: 输入数据大小(n_x, m)
:return:
predictions -- 模型预测向量(红色:0 / blue: 1)
"""
A2, cache = forward_propagation(X, parameters)
predictions = A2 > 0.5
return predictions
def test_anther_hidden():
"""
使用不同的隐层训练
:return:
"""
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
parameters = nn_model(X, Y, n_h, num_iterations=1000)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
if __name__ == "__main__":
parameters = nn_model(X, Y, n_h=4, num_iterations=10000, print_cost=True)
predictions = predict(parameters, X)
print 'Accuracy: %d' % float(
(np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%'
# test_anther_hidden()
参考资料
该笔记是学习吴恩达老师的课程写的。初学者入门,如有理解有误的,欢迎批评指正!