夜雨飘零

说明

这个是使用PaddlePaddle训练cifar10数据集的一个例子

问题1：网络结构

问题：计算每层网络结构和输入输出尺寸和参数个数。不加BN？更深？每层的尺寸变化？更多结构？

def convolutional_neural_network(img):
    print('输入层的shape：', img.shape)
    conv_pool_1 = fluid.nets.simple_img_conv_pool(
        input=img,
        filter_size=5,
        num_filters=20,
        pool_size=2,
        pool_stride=2,
        act="relu")
    print('第一层卷积池化层输出shape：', conv_pool_1.shape)
    conv_pool_1 = fluid.layers.batch_norm(conv_pool_1)
    conv_pool_2 = fluid.nets.simple_img_conv_pool(
        input=conv_pool_1,
        filter_size=5,
        num_filters=50,
        pool_size=2,
        pool_stride=2,
        act="relu")
    print('第二层卷积池化层输出shape：', conv_pool_2.shape)
    conv_pool_2 = fluid.layers.batch_norm(conv_pool_2)
    conv_pool_3 = fluid.nets.simple_img_conv_pool(
        input=conv_pool_2,
        filter_size=5,
        num_filters=50,
        pool_size=2,
        pool_stride=2,
        act="relu")
    print('第三层卷积池化层输出shape：', conv_pool_3.shape)
    prediction = fluid.layers.fc(input=conv_pool_3, size=10, act='softmax')
    print('全连接层输出shape：', prediction.shape)
    return prediction

卷积层输出计算公式：

• 输入shape：$(N,C_{in},H_{in},W_{in})$
• 卷积核shape：$(C_{out},C_{in},H_f,W_f)$

$H_{out}=\frac{(H_{in}+2padding-(dilation(H_f-1)+1))}{stride}+1$

$W_{out}=\frac{(W_{in}+2padding-(dilation(W_f-1)+1))}{stride}+1$

• 输出shape：$(N,C_{out},H_{out},W_{out})$

池化层输出计算公式：

• 输入shape：$(N,C,H_{in},W_{in})$
• 池化shape：$(1,1,ksize,ksize)$

$H_{out}=\frac{H_{in}-ksize}{stride}+1$

$W_{out}=\frac{W_{in}-ksize}{stride}+1$

• 输出shape：$(N,C,H_{out},W_{out})$

参数大小计算公式：

$psize=C_{out}*C_{in}ksizeksize$

答1： 本网络的的输入数据的shape为(128, 3, 32, 32)，所以输出如下：

• 第一层的卷积层输出shape：(128, 20, 28, 28)，参数大小为：$2035*5=1500$
• 第一层的池化层输出shape：(128, 20, 14, 14)
• 第二层的卷积层输出shape：(128, 50, 10, 10)，参数大小为：$50205*5=25000$
• 第二层的池化层输出shape：(128, 50, 5, 5)
• 第三层的卷积层输出shape：(128, 50, 1, 1)，参数大小为：$50505*5=62500$
• 第三层的池化层输出shape：(128, 50, 1, 1)
• 最后的全连接层输出shape：(128, 10)，参数大小为：$50*10=500$
• 总参数大小：$1500+25000+62500+500=89500$

PaddlePaddle的网络输出

输入层的shape： (-1, 3, 32, 32)
第一层卷积池化层输出shape： (-1, 20, 14, 14)
第二层卷积池化层输出shape： (-1, 50, 5, 5)
第三层卷积池化层输出shape： (-1, 50, 1, 1)
全连接层输出shape： (-1, 10)

答2：
在没有使用BN层之前：

• 参数的更新，使得每层的输入输出分布发生变化，称作ICS（Internal Covariate Shift）
• 差异hui会随着网络深度增大而增大
• 需要更小的学习率和较好的参数进行初始化

加入了BN层之后：

• 可以使用较大的学习率
• 可以减少对参数初始化的依赖
• 可以拟制梯度的弥散
• 可以起到正则化的作用
• 可以加速模型收敛速度

用BN层的训练情况：

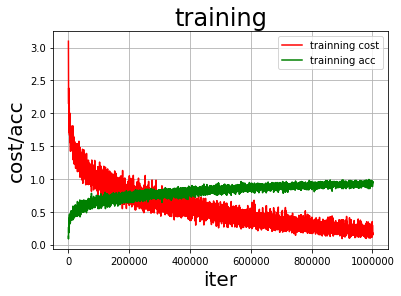
不使用BN层的训练情况：

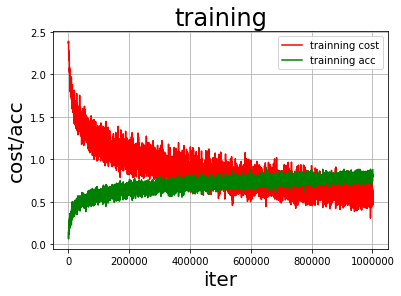
从图中可以看出使用BN层的准确率更高，训练过程中损失值和准确率的幅度更加小。

答3： 因为该网络的第三层卷积池化层输出的宽和高都是1，所以不能再增加卷积池化层，如果再使用卷积池化层，就会报以下的错误。

EnforceNotMet: Due to the settings of padding(0), filter_size(5), dilation(1) and stride(1), the output size is less than 0, please check again. Input_size:1