深度学习的实践方面

1. 如果有10,000,000个例子，数据集拆分一般是98%训练，1%验证，1%测试。
2. 验证和测试的数据集通常是来自同样的分配。
3. 如果神经网络模型有很大的差异，一般的解决办法是增加数据集和添加正则。
4. 当训练集错误较小，而验证集较大时，通常是增加正则lambda、增加数据集。
5. 当增加正则化超参数lambda时，权重会被推向更小，接近0.
6. 将参数keep_prob从（比如说）0.5增加到0.6可能会导致减少正则效应、最终导致更小的训练集数据的错误。
7. 增加训练集、添加Dropout、加正则可以减少方差（减少过度拟合）。
8. 权重衰减是一种正则化技术(如L2正规化), 导致梯度下降在每次迭代中收缩权重。
9. 我们归一化输入的X，是因为这个可以使得损失函数更快地进行优化。
10. 在测试使用反向dropout方法时，不要使用dropout（不要使用随机消除单位），也不要在训练中使用计算中保留的1/keep_prob因子。

优化算法

1. 当输入是来自第8个小批次的第7个示例时，表示第3层的激活的符合是：$a^{[3]{8}(7)}$。
2. 小批量梯度下降（在单个小批量上计算）的一次迭代比批量梯度下降的迭代快。
3. 最好的小批量大小通常不是1而不是m，而是介于两者之间。一、如果最小批量为1，则会小批量样本中失去向量化的好处。二、如果最小批量为m，则最终会产生批量梯度下降，该批量梯度下降处理完成之前必须处理整个训练集。
4. 假设学习算法的成本$J$，绘制为迭代次数的函数，如下所示：
   
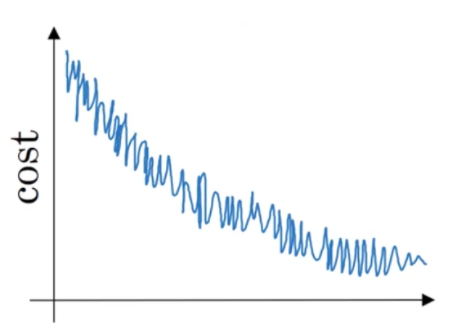
   从图中可以得知如果是使用小批量梯度下降法，看来是可以接受的，如果是使用批量梯度下降，有些事情是错误的。
5. 假设1月前三天卡萨布兰卡的气温相同：
   1月1日：$\theta_1 = 10^o C$
   1月2日： $\theta_2 = 10^o C$
   假设使用指数加权平均$\beta=0.5$跟踪温度：$v_0 = 0, v_t = \beta v_{t-1} +(1-\beta)\theta_t$。可以得到2天后的值：$v_2 = 7.5$，以及其修正偏差的值是：$v_2^{corrected} = 10$。
6. $\alpha = e^t \alpha_0$不是一个好的学习率衰退的方法，其中t是epoch号码。比较好的方法有：$\alpha = 0.95^t \alpha_0$，$\alpha = \frac{1}{\sqrt{t}} \alpha_0$，$\alpha = \frac{1}{1+2*t} \alpha_0$ 这些。
7. 伦敦温度数据集上使用指数加权平均值。使用以下来跟踪温度：$v_{t} = \beta v_{t-1} + (1-\beta)\theta_t$。下面的红线是用来计算的$\beta=0.9$。
   
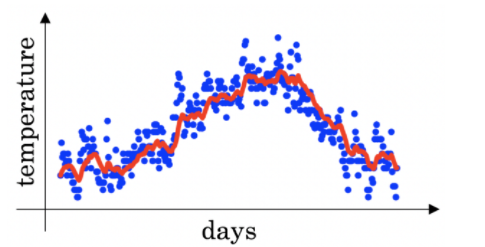
   增加$\beta$会将红线稍微向右移；降低$\beta$将在红线内产生更多的振荡。
8. 图中：
   
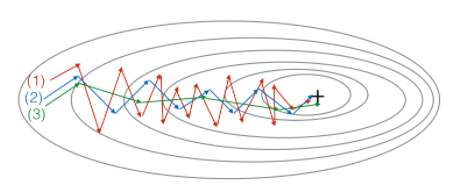
   这个图是梯度下降、动量梯度下降（$\beta = 0.5$）和动量梯度下降（$\beta= 0.9$）产生的。其中（1）是梯度下降。（2）是动量梯度下降（小$\beta$）。（3）是动量梯度下降（大$\beta$)
9. 假设深度网络中的批量梯度下降时间过长，为找到对于成本函数实现较小值的参数值$\mathcal{J}(W^{[1]},b^{[1]},..., W^{[L]},b^{[L]})$。可以使用以下技术找到取得较小值的参数值$\mathcal{J}$：一、尝试调整学习率$\alpha$；二、尝试更好的随机初始化权重；三、尝试使用小批量梯度下降；四、尝试使用Adam。
10. 关于Adam的一些正确的说法：一、学习速率超参数$\alpha$在Adam通常需要调整；二、我们通常使用$\beta_1,\beta_2$和$\varepsilon$作为Adam ($\beta_1=0.9, \beta_2=0.999, \varepsilon = 10^{-8}$)超参数的默认值；三、Adam结合了RMSProp的优点和动量。

超参数调整，批量标准化，编程框架

1. 在大量超参数中进行搜索，通常使用随机值而不是网格中的值。
2. 不是每个超参数都会对训练产生巨大的负面影响，比如学习率，比其他参数更重要。
3. 在超参数搜索过程中，无论您是尝试照顾一个模型（“熊猫”策略）还是平行训练大量模型（“鱼子酱”），主要取决于可以访问的计算能力的数量。
4. 如果$\beta$（动量超参数）介于0.9和0.99之间，推荐使用以下方法用于对$\beta$值进行抽样：

r = np.random.rand()
beta = 1-10**(- r - 1)

5. 当找到非常好的超参数之后，并不是一劳永逸的，当网络或者其他超参数改变之后，还要再次重新调整它们的。
6. 在批量标准化中，如果将其应用于$l$你的神经网络的第一层，$z^{[l]}$是规范化的公式。
7. 在规范化公式中$z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \varepsilon}}$，使用epsilon是避免$z^{(i)} - \mu$被零除。
8. 在关于$gamma$和$beta$在批准规范中，他们可以使用Adam，动量梯度下降或RMSprop，而不仅仅是渐变下降来学习；他们设置线性变量的均值和方差是从$z^{[l]}$的给定图层。
9. 执行必要的规范化时，使用$\mu$和$\sigma^2$估计在训练期间的小批量的指数加权平均。
10. 在深度学习框架中，即使项目目前是开源的，项目的良好治理也有助于确保项目长期保持开放，而不是被封闭或修改为只有一家公司受益；通过编程框架，用户可以使用比高级级语言（如Python）更少的代码行编写深度学习算法。