目录

@[toc]

深度学介绍

1. AI比喻新电是是因为AI就像大约100年前的电力一样，正在改变多个行业，如： 汽车行业，农业和供应链。
2. 深度学习最近起飞的原因是：硬件的开发，特别是GPU的计算，是我们获得更多的计算能力；深度学习已在一些重要的领域应用，如广告，语音识别和图像识别等等；目前数字化的时代使得我们拥有更多的数据。
3. 关于迭代不同ML思想的图：
   

• 这个思维图能够快速尝试想法，可以让深度学习工程师更快速地迭代自己的想法；
• 可以加快团队迭代一个主意的时间；深度学习算法的新进展使得我们能更好地训练模型，即使不改变CPU或者GPU硬件。

4. 寻找模型的特征是获取良好性能的关键，虽然经验可以提供帮助，但是需要多次迭代来建立一个良好的模型。
5. ReLU激活函数的图表如下：
   
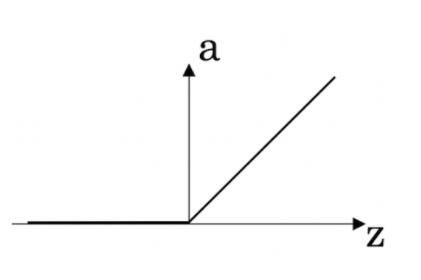
6. 猫的识别是一个“非结构化”的数据例子；统计不同城市人口，人均GDP，经济增长的人口统计数据集是反映图像，音频或者文本数据集的“结构化”数据的一个例子。
7. 为什么使用RNN（循环神经网络）作为机器翻译，这是因为RNN是一个可以被训练的监督学习的问题；RNN的输入和输出是一个序列，翻译就是从一种语言序列映射到另一种语言的序列。
8. 这张手工绘制的图像，x轴是指数据量，y轴是指算法的性能
   
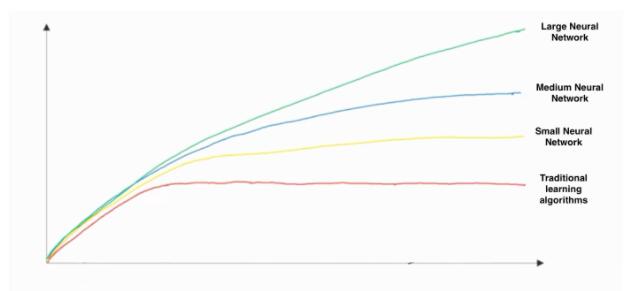
   • 同时在图像中可以看出增加训练数据是不会影响算法的性能的，引入更多的数据对模型总是有益的；
   • 有知道增加神经网络的大小通常不会影响算法的性能，大型的网络通常比小网络表现要好。

神经网络基础

1. 神经元计算一个线性函数(z = Wx + b),后跟一个激活函数（sigmoid，tanh，ReLU，...）
2. 使用numpy直接计算矩阵，这跟np.dot(a,b)不同，直接运算时按照广播的方式运算的，使员工np.dot(a,b)是按照平时矩阵的计算方式的。
3. 假设img是一个(32,32,3)的数组，代表具有3个颜色通道红色，绿色和蓝色的3232的图像，重塑这个成为列向量应该为：x = img.reshape((3232*3,1))
4. "Logistic Loss"函数应该是：
   
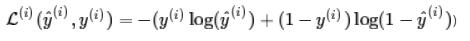
5. 以下图像的计算过程
   
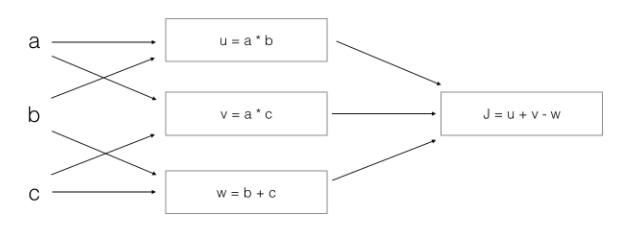
   应该是：

$$
J = u + v - w = (ab)+(ac)-(b+c)
= a*(b+c)-(b+c) = (a-1)*(b+c)

$$

浅层神经网络

1. $a^{12}$表示激活向量的第2层的第12个的训练样本。
2. $X$每列都是一个训练样本的矩阵
3. $a_4^{[2]}$表示第2层的第4个的激活输出
4. $a^{[2]}$表示第2层激活向量
5. tanh激活函数通常比隐层单元的sigmoid激活函数效果要好，因为tanh的输出范围在(-1,1)，其平均值更接近零，因此它能把数据更集中传到下一层，使学习变得更简单。
6. Sigmoid函数的输出在0和1之间，这使得它是二分类的非常好的一个选择，当输出低于0.5时，可以归类为0；当输出高于0.5时，可以归类为1。使用tanh函数也可以，但是tanh的函数在-1和1之间，操作不太方便。
7. Logistic回归因为没有隐层，如果将权重初始化为零，则Logistic回归中的第一个样本输出将是零，但是Logistic回归的导数取决于不是零，而是输入的x(因为没有隐层)。因此在第二次迭代中，如果x不是常量向量，则权重值遵循x的分布且彼此不同。
8. 当tanh激活函数的输入远离零时，其梯度就非常接近于零，因为此时的tanh斜率接近零。
9. 一个隐藏层的神经网络：
   
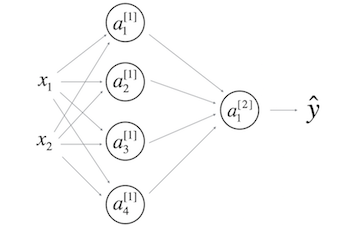
   $b^{[1]}$的形状应该是(4,1)；$b^{[2]}$的形状应该是(1,1)；$W^{[1]}$的形状应该是(4,2)；$W^{[2]}$形状应该是(1,4)
10. 在$l$层中，其中$1<=l<=L$，对$l$层前向传播正确矢量化的公式是：
    

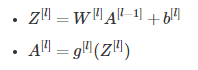
深度神经网络

1. 在前向传播和反向传播中使用“cache”，是为了记录前向传播单元计算的值，然后传送给反向传播的单元，因为在使用链式法则计算导数时使用到。
2. 属于超参数的是：迭代次数，学习率，神经网络$L$的层数，隐层的数量。
3. 深层神经网络比浅层神经网络计算更加复杂的输入特征。
4. 以下这个网络是4层的神经网络，有3个隐层
   
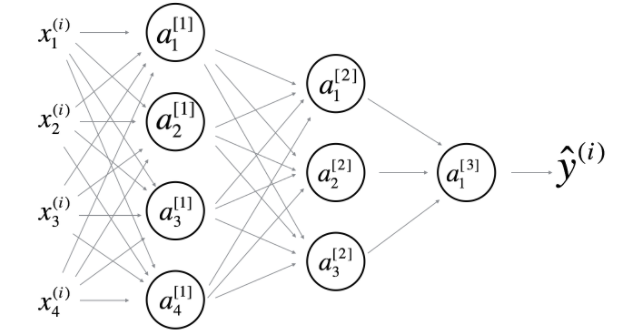
   计算层数的方式：层数=隐层+1，输入层和输出层不属于隐层。
5. 在前向传播中，前向函数需要知道使用的是什么激活函数（Sigmoid，tanh，ReLU，等等），因为在反向传播中需要知道是使用了什么激活函数才能正确计算导数。
6. 使用浅层网络电路进行计算，需要一个大型的网络（我们通过网络的逻辑门数来测量大小），但是计算深层的电路的话，只需要一个指数规模比较小的网络。
7. 以下是一个2层隐层的神经网络结构图：
   [外链图片转存失败(img-ggjHJvwx-1563949655959)(https://note.youdao.com/yws/api/personal/file/AE2D93A09BC54E4AB3A986056C2B4DDB?method=download&shareKey=2e6f6ed04ebd0c5c7e5e3fa21d71b3f2)]
   它具有：(i)、$W^{[1]}$的形状是(4,4)（计算方式是：$W^{[l]} = (n^{[l]},n^{[l-1]})$），同样$W^{[2]}$的形状是(3,4)，$W^{[3]}$的形状是(1,3)；(ii)、$b^{[1]}$的形状是(4,1)（计算方式是：$b^{[l]} = (n^{[l]},1)$），同样$b^{[2]}$的形状是(3,1)，$b^{[3]}$的形状是(1,1)
8. 假设我们存储的值$n^{[l]}$在一个名为layers的数组中，如下所示：layer_dims = [$n_x$，4,3,2,1]。因此，第1层有四个隐藏单元，第2层有三个隐藏单元，依此类推。则使用下面的for循环初始化模型的参数：

for(i in range(1, len(layer_dims))):
  parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i-1])) * 0.01
  parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01

该笔记是学习吴恩达老师的课程写的。初学者入门，如有理解有误的，欢迎批评指正！