上溢和下溢

• 下溢(underflow)是一种极具毁灭性的舍入误差.当接近零的数被四舍五入为零时发生下溢
• 上溢(overflow)是一种极具破坏力的数值错误形式.当大量级的数被近似为$\infty$或者$-\infty$时发生上溢,进一步的运算通常会导致这些无限值变成非数字.
• softmax 函数(softmax function)可以对上溢和下溢进行数值稳定的一个函数,softmax函数经常用于预测与Multinoulli分布相关联的概率,定义为:

基于梯度的优化方法

大多数深度学习算法都涉及某种形式的优化.优化指的是改变$x$以最小化或最大化某个函数$f(x)$的任务.我们通常以最小化$f(x)$指代大多数最优化问题,最大化可以经由最小化算法最小化$-f(x)$来实现
我们把要最小化或最大化的函数称为目标函数(objective function)或者准则(criterion).当我们对其进行最小化时,也把它称为代价函数(cost function),损失函数(loss function)或者误差函数(error function)

导数

导数（derivative）：设函数$y=f(x)$在点$x_0$的某邻域$U(x_0)$内有定义,当自变量$x$在点$x_0$处取得增量$\triangle x$($\triangle x \neq 0$ 且$x_0+\triangle x \in U(x_0)$)时,相应的函数$y$取得增量:

$$
\triangle y = f(x_0 + \triangle x)-f(x_0)\tag{1}

$$

若极限

$$
\lim_{\triangle x \rightarrow0}\frac{\triangle y}{\triangle x} = \lim_{\triangle x \rightarrow0}\frac{f(x_0 + \triangle x)-f(x_0)}{\triangle x}\tag{2}

$$

存在,则称函数$y=f(x)$在点$x_0$可导,并称此极限值为函数$y=f(x)$在点$x_0$的导数,记作$f^\prime(x_0)$或者$\left.\frac{dy}{dx}\right | _{x=x_0}$
由上面的定义可得若曲线$y=f(x)$存在一点$(x_0,y_0)$,并且在这点上可导,导数为$f^\prime(x_0)$,那么导数$f^\prime(x_0)$就是该点的斜率.
梯度下降(gradient descent)导数对最小化一个函数很有用,当$\triangle x$足够小时,$f(x-\triangle x{\rm sign}(f^\prime(x)))$是比$f(x)$小的,因此我们可以将$x$往导数的反方向移动一小步来减小$f(x)$.这种技术称为梯度下降

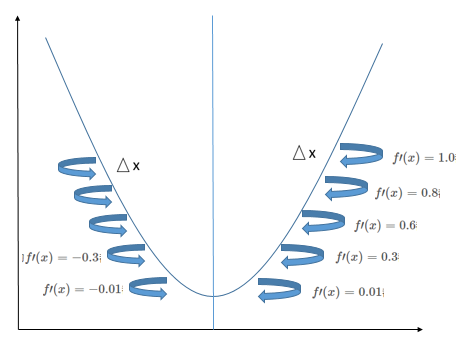
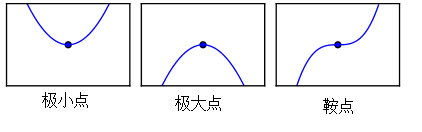
在不断重复上面操作后,最终可以得到$f^\prime(x)=0$,改点称为临界点(critical point)或驻点(stationary),这个驻点可能是极大点(maximum),或者是极小点(minimum),还有可能是鞍点(saddle point),还要进一步计算.

1. 当驻点的左边的$\triangle x$距离的$f^\prime(x)$小于0,而驻点的右边边的$\triangle x$距离的$f^\prime(x)$大于0,则该驻点是极小值
2. 当驻点的左边的$\triangle x$距离的$f^\prime(x)$大于0,而驻点的右边边的$\triangle x$距离的$f^\prime(x)$小于0,则该驻点是极大值
3. 当驻点的距离左右两边的$\triangle x$距离的$f^\prime(x)=$都小于0或都大于0,则该驻点是鞍点
   

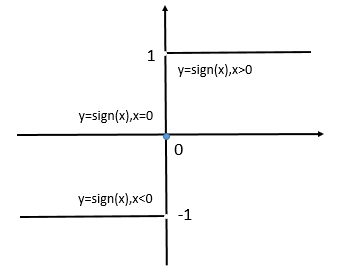
在上面用到了${\rm sign}$函数,下面的就是${\rm sign}$定义:

$$
{\rm sign}(x) =
\left{
\begin{matrix}
1,x>0 \
0,x=0 \
-1,x<0
\end{matrix}
\right. \tag{3}

$$

${\rm sign}$函数的坐标图：

偏导数

当函数只有二维输入时，其只有一个驻点，所以这个驻点就是它的最小点或者最大点。但是通常遇到更多的是多维输入的函数，它具有多个驻点，所以它有多个极小点和极大点，如下图。所以通过上面的方法很难找到最大点或者最小点。

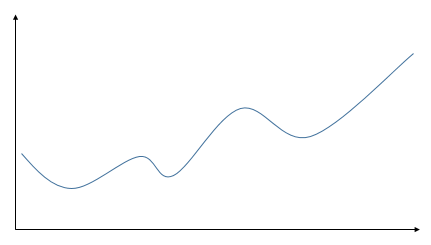
针对具有多维输入的函数，我们就需要用到偏导数(partial derivative)的概念了。
设函数$z=f(x,y)$在点$(x_0,y_0)$的某个领域内有定义，当$y$固定在$y_0$而$x$在$x_0$处有增量$\triangle x$时，相应地函数有增量

$$
f(x_0+\triangle x,y_0)-f(x_0,y_0)\tag{4}

$$

如果有极限

$$
\lim_{\triangle x \rightarrow 0}\frac{f(x_0+\triangle x,y_0)-f(x_0,y_0)}{\triangle x}\tag{5}

$$

存在，则称此极限为函数$z=f(x,y)$在点$(x_0,y_0)$处对$x$的偏导数，记作：

$$
\left.\frac{\partial f}{\partial x}\right|_{x=x_0,y=y0}\quad 或\quad f^\prime_x(x_0,y_0)\tag{6}

$$

同理，函数$z=f(x,y)$在点$(x_0,y_0)$处对$y$的偏导数为：

$$
f^\prime y(x_0,y_0) = \lim{\triangle y \rightarrow 0}\frac{f(x_0,y_0+\triangle y)-f(x_0,y_0)}{\triangle y}\tag{7}

$$

例求$f(x,y)=x^2+3xy+y^2$在点(2,1)处的偏导数$f_x(2,1),f_y(2,1)$.
解：把$y$看作常数，对$x$求导得到

$$
f_x(x,y)=2x+3y\tag{8}

$$

把$x$看作常数，对$y$求导得到

$$
f_y(x,y)=3x-2y\tag{9}

$$

代入$x=2,y=1$，故所求偏导数为：

$$
f_x(2,1) = 7,f_y(2,1)=4\tag{10}

$$

梯度(gradient)是相对一个向量求导的导数：$f$的导数是包含所有偏导数的向量，记作$\nabla_xf(x)$。梯度的第$i$个元素是$f$关于$x_i$的偏导数。在多维情况下，临界点是梯度中所有元素都为零的点。

约束优化

有时候,在$x$的所有可能值下最大化或者最小化一个函数$f(x)$不是我们所希望的,相反,我们可能希望在$x$的某些集合${\Bbb S}$中找到$f(x)$的最大值或者最小值,这个称为约束优化(constrained optimization)
Karush-Kuhu-Tucker(KKT)方法是针对约束优化非常通用的解决方案,KKT方法是Lagrange乘子法(只允许等式约束)的推广

参考资料

1. lan Goodfellow,Yoshua Bengio,Aaron Courville.深度学习(中文版).赵申剑,黎彧君,符天凡,李凯,译.北京:人民邮电出版社
2. 郭游瑞,徐应祥,任阿娟,赵志琴.高等数学简明教程.上海:复旦大学出版社